Les unités

Cherchez à comprendre comment vous pouvez construire toutes les valeurs que l'on peut coder sur trois bits à partir des valeurs que l'on peut coder sur deux bits.

Puis cherchez de même à comprendre comment vous pouvez construire toutes les valeurs que l'on peut coder sur quatre bits à partir des valeurs que l'on peut coder sur trois bits.

Généralisez...

Un bit peut prendre deux valeurs : 0 ou 1.

Avec deux bits : on part de l'état du premier bit (0 ou 1) et on complète par l'état du second bit.

• Soit le premier bit est à 0 et on peut compléter sur le second bit par 0 ou 1, ce qui donne : 00 ou 01.
• Soit le premier bit est à 1 et on peut compléter sur le second bit par 0 ou 1, ce qui donne : 10 ou 11.

Avec trois bits : on part de l'état des deux premiers bits et on complète par l'état du troisième.

• L'état 00 conduit aux deux états 000 et 001.
• L'état 01 conduit aux deux états 010 et 011.
• L'état 10 conduit aux deux états 100 et 101.
• L'état 11 conduit aux deux états 110 et 111.

Le nombre de mots de longueur 3 bits est donc le double du nombre de mots de longueur 2 bits.

De la même façon, chaque mot écrit sur 3 bits peut donner lieu à deux mots sur quatre bits : un mot en complétant le mot de longueur trois bits par un 0, et un autre mot en complétant par 1.

Le nombre de mots sur 4 bits sera donc le double du nombre de mots sur 3 bits.

On obtient les états à n bits en complétant chacun des états possibles à n-1 bits par l'une ou l'autre (0 ou 1) des possibilités pour le bit ajouté.

On voit donc que l'on multiplie par deux le nombre d'états possibles à chaque fois que l'on ajoute un bit.

Comme pour un bit, le nombre d'états est égal à 2, il est égal à 2× 2 = 2 ² pour 2 bits, à 2²×2 = 2³ pour 3 bits, à 2³×2 = 2⁴ pour 4 bits, ... Et de façon générique, on a deux 2ⁿ états possibles sur une longueur de n bits.

Il s'agit du même problème que dans l'exercice précédent.

La composante R peut prendre 2⁸ valeurs différentes.

La composante G peut prendre 2⁸ valeurs différentes.

A chaque valeur de la composante R, on peut associer n'importe quelle valeur de la composante G. Cela fait donc déjà 2⁸ × 2⁸ valeurs possibles.

La composante B peut prendre 2⁸ valeurs différentes.

On peut compléter chacune des 2⁸ × 2⁸ valeurs (R,G) par n'importe quelle valeur de la composante B. Cela fait donc 2⁸ × 2⁸ × 2⁸ = 16 777 216 valeurs possibles.

On peut plus brièvement remarquer que le codage se fait sur une longueur de 3×8=24 bits.

D'après l'exercice précédent, on peut donc coder 2²⁴ couleurs. On retrouve bien entendu nos plus de 16 millions de couleurs obtenues par le décompte précédent.

Avec 32 bits, on peut coder 2³² = 4 294 967 296 (un peu plus de 4 milliards) adresses distinctes (en fait certains codes sont réservés à des rôles particuliers, mais cela ne fera pas vraiment de différence pour cet exercice)

Avec 128 bits, on peut coder 2¹²⁸ adresses (soit plus de 3 * 10³⁸ adresses).

Avec un milliard d'adresses par seconde, on épuiserait le potentiel de l' IPv4 en moins de 5 secondes.

Avec l'IPv6, il nous faut $\frac{2^{128}}{10^9} \text{secondes} = \frac{2^{128}}{10^9 \times 3600 \times 24 \times 365} \text{années}$ soit plus de 10²² années. A titre de comparaison, l'âge de l'univers est estimé à environ 15.10 ⁹ années. Il faudrait donc 700 milliards de fois l'âge de l'univers pour épuiser le potentiel de l'adressage IPv6 sous ces conditions !

Pour comprendre ce qu'est le routage IP, vous pouvez lire cette page.

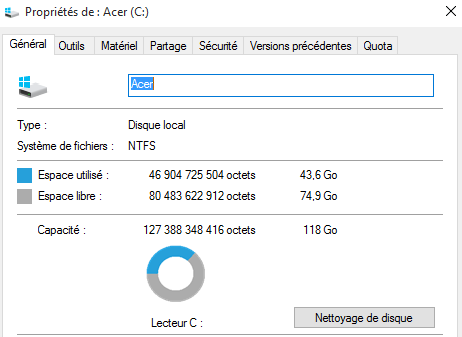
128 Gio = 128 × 2³⁰ octets ≈ 137,5 × 10⁹ octets. Environ 137,5 Go.

100 Go = 100 × 10⁹ octets ≈ 93,13 × 2³⁰, soit environ 93,13 Gio.

Le nombre utilisé en Go est toujours supérieur puisque 1 Go est inférieur à 1 Gio.

46 904 725 504 octets correspondent évidemment à 46,9 Go (en arrondissant) et non à 43,6 Go.

Par contre 46 904 725 504 octets est approximativement égal à 43,68× 2³⁰ octets.

Microsoft confond donc les Go et les Gio. L'espace utilisé est de 43,68 Gio.

A titre de comparaison, ci-dessous ce qu'affiche linux pour une clef usb de 4 Go et ce qu'affiche windows.
.

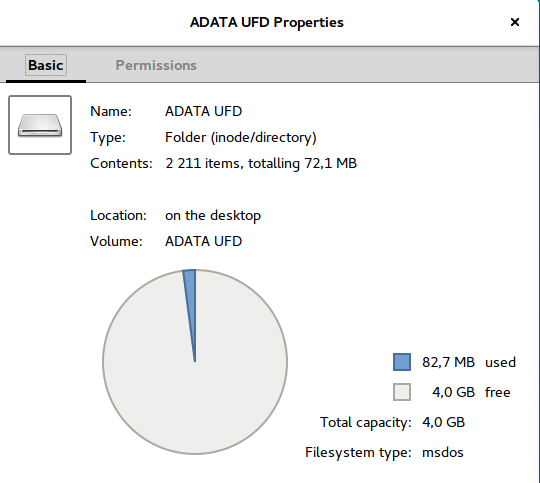
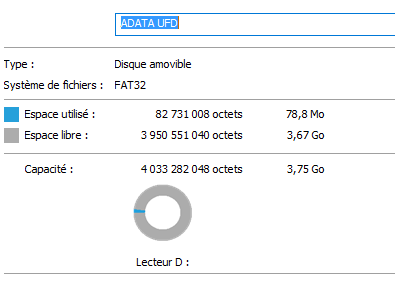
Les indications en octets sont corrects (heureusement) pour windows. Mais il est plus naturel de lire les indications en Go : la signification de nombres courts est en effet plus facile à appréhender. Un utilisateur peut donc être facilement trompé par la lecture de l'indication windows, tandis qu'elle est correcte sous linux.

Une discussion sur un forum liée à ce problème ici.

Nombre de chansons

1 To = 10¹² octets.

4 Mo = 4 × 10⁶ octets.

$\frac{10^{12}}{4 \times 10^6} = 0.25 \times 10^6 = 25 \times 10^4$

On peut donc stocker environ 250 000 chansons de ce type sur le disque de 1 To.

$250000 \times 4 = 1 000 000$ , un million de minutes.

$\frac{1000000}{60*24} \approx 694$ , environ 694 jours.

Pas loin de deux années de musique !

Avec LibrOffice, j'ai obtenu un poids de 8225 octets. Avec un fichier txt, un poids de 9 octets.

Un fichier 900 fois plus lourd avec le traitement de texte !!

1 Po = 10¹⁵ octets.

500 To = 500 × 10¹² octets.

En un an, le nombre d'octets enregistrés est : 500 × 10¹² × 365.

Soit 1825 × 10¹⁴ octets ou encore 182.5 × 10¹⁵ octets.

Plus de 182 Po de données en 2012...