Capacité 22 a☘

Déterminer graphiquement des images.

A retenir☘

La représentation graphique d'une fonction $f$ définie sur un ensemble K de nombres est l'ensemble des points $M$ dont les coordonnées sont de la forme $(x~;~f(x))$ ( $x$ parcourant K).

Lire graphiquement l'image d'un nombre $a$ par une fonction $f$ consiste donc à lire l'ordonnée du point de la courbe ayant son abscisse égale à $a$ .

En d'autres termes: Si A est un point de la courbe et si $x_A = a$ , alors $y_A = f(a)$ .

Question☘

Lire graphiquement:

l'image de 1 par la fonction f représentée.
f(2)

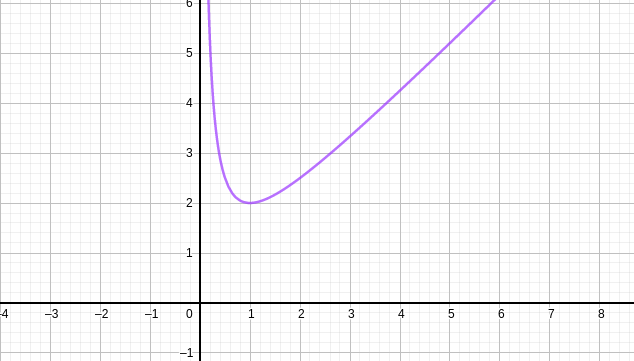
Solution

L'image de 1 est $f(1) \approx 2$ .

$f(2) \approx 2,5$

Question☘

Lire graphiquement:

l'image de 0 par la fonction f représentée.
f(1)
l'image de -1 par la fonction f représentée.

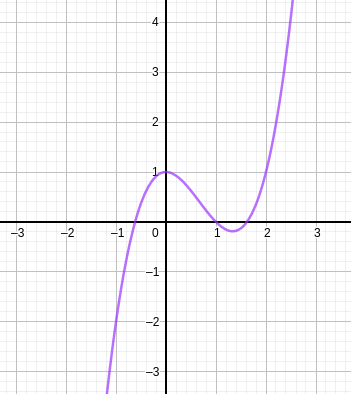
Solution

L'image de 0 est $f(0) \approx 1$ (point A(0;1) sur la courbe)

$f(1) \approx 0$ (point B(1;0) sur la courbe)

L'image de -1 est $f(-1) \approx -2$ (point C(-1;-2) sur la courbe)

Question☘

Lire graphiquement:

l'image de 1 par la fonction f représentée.
f(3)
l'image de -3 par la fonction f représentée.

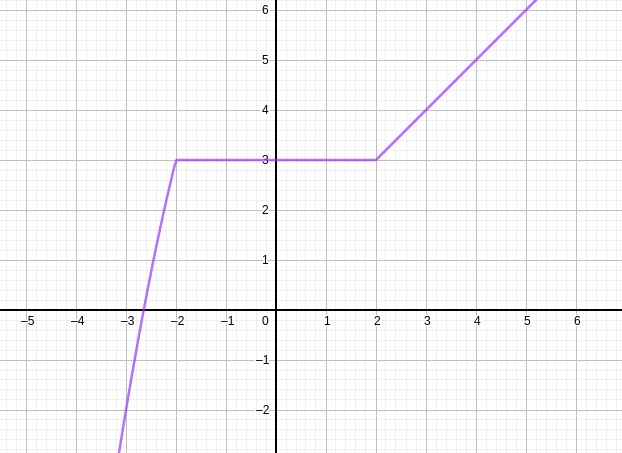
Solution

L'image de 1 est $f(1) \approx 3$ (point A(1;3) sur la courbe)

$f(3) \approx 4$ (point B(3;4) sur la courbe)

L'image de -3 est $f(-3) \approx -2$ (point C(-3;-2) sur la courbe)

Question☘

Lire graphiquement:
- l'image de 1 par la fonction f représentée.
- f(2)

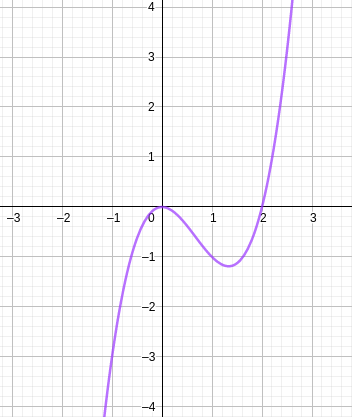
Solution

L'image de 1 est $f(1) \approx -1$ (point A(1;-1) sur la courbe).

$f(2) \approx 0$ (point B(2;0) sur la courbe).