Capacité 27a☘
Tracer une droite donnée par son équation réduite.
A savoir☘
Une droite étant donnée par son équation réduite, pour en tracer une représentation, il suffit de placer deux points dont les coordonnées satisfont l'équation de la droite.
Question☘
Représenter dans un repère orthonormé la droite d'équation réduite y = \frac{1}{3}x + 2.
Solution
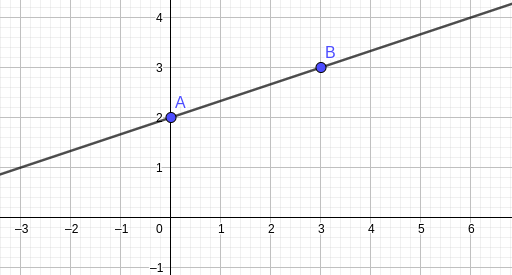
Avec x=0, on obtient y=2. Le point A(0;2) est donc un point de la droite.
Avec x=3, on obtient y=3. Le point B(3;3) est donc un point de la droite.
On place ces deux points dans un repère et on a ainsi une représentation de la droite.
Question☘
Représenter dans un repère orthonormé la droite d'équation réduite y = \frac{1}{4}x - \frac{1}{3}.
Solution
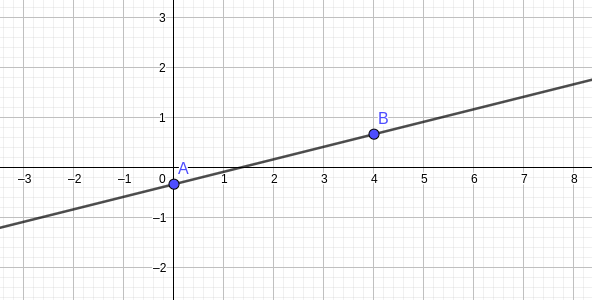
Avec x=0, on obtient y=- \frac{1}{3}. Le point A(0;-\frac{1}{3}) est donc un point de la droite.
Avec x=4, on obtient y=\frac{2}{3}. Le point B(4;\frac{2}{3}) est donc un point de la droite.
On place ces deux points dans un repère et on a ainsi une représentation de la droite.
Question☘
Représenter dans un repère orthonormé la droite d'équation réduite y =2x - \frac{2}{3}.
Solution
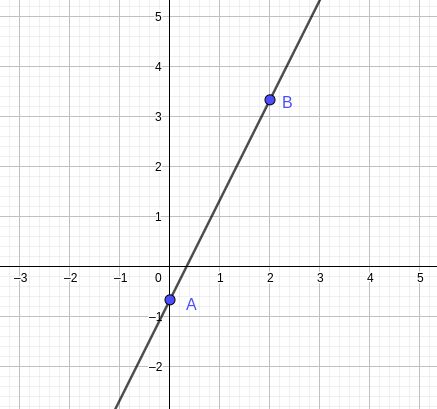
Avec x=0, on obtient y=- \frac{2}{3}. Le point A(0;-\frac{2}{3}) est donc un point de la droite.
Avec x=2, on obtient y=\frac{10}{3}. Le point B(2;\frac{10}{3}) est donc un point de la droite.
On place ces deux points dans un repère et on a ainsi une représentation de la droite.
Question☘
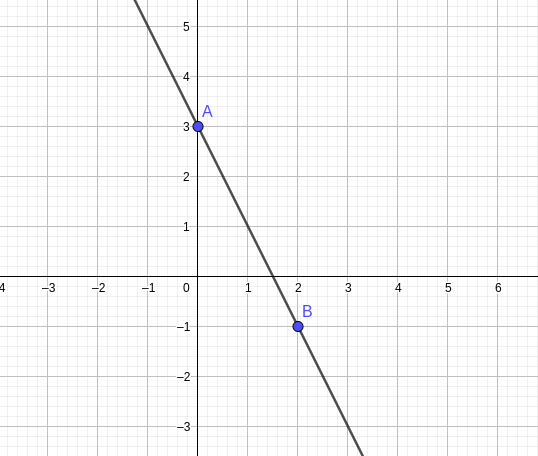
Représenter dans un repère la droite d'équation réduite y = -2x + 3.
Solution
Avec x=0, on obtient y=3. Le point A(0;3) est donc un point de la droite.
Avec x=2, on obtient y=-1. Le point B(2;-1) est donc un point de la droite.
On place ces deux points dans un repère et on a ainsi une représentation de la droite.
Question☘
Représenter dans un repère la droite d'équation réduite y = \frac{1}{4}x +1.
Solution
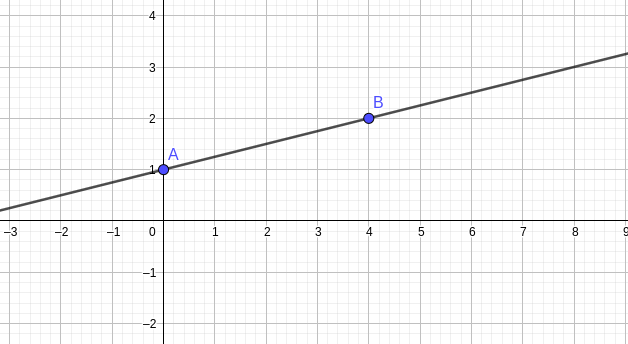
Avec x=0, on obtient y=1. Le point A(0;1) est donc un point de la droite.
Avec x=4, on obtient y=2. Le point B(4;2) est donc un point de la droite.
On place ces deux points dans un repère et on a ainsi une représentation de la droite.