Capacité 27b☘

Tracer une droite donnée par un point et son coefficient directeur.

A savoir☘

Une droite ayant un coefficient directeur $m$ est dirigée par le vecteur $\overrightarrow{u}(1~;~m)$ .

Si cette droite passe par un point $A(x_A~;~y_A)$ , on représente le vecteur $\overrightarrow{u}(1~;~m)$ avec origine le point $A$ .

L'extrémité du représentant d'origine $A$ de ce vecteur est le point $B\left( x_A +1 ~;~ y_A +m \right)$ , point de la droite.

Question☘

Représenter dans un repère orthonormé la droite de coefficient directeur 2 passant par le point $A(1~;~3)$ .

Solution

On commence par placer le point $A$ donné.

La droite ayant un coefficient directeur $m$ est dirigée par le vecteur $\overrightarrow{u}(1~;~m)$ . On représente donc le vecteur $\overrightarrow{u}(1~;~2)$ ayant pour origine le point $A$ .

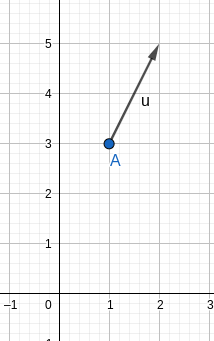
Remarque: l'extrémité du représentant du vecteur dessiné est le point $B(x_A+1~;~y_A+m) = B(2~;~5)$ .

D'où une représentation de la droite:

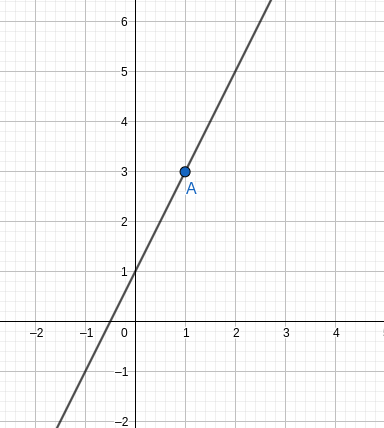
Question☘

Représenter dans un repère orthonormé la droite de coefficient directeur -3 passant par le point $A(-2~;~0)$ .

Solution

On commence par placer le point $A$ donné.

La droite ayant un coefficient directeur $m$ est dirigée par le vecteur $\overrightarrow{u}(1~;~m)$ . On représente donc le vecteur $\overrightarrow{u}(1~;~-3)$ ayant pour origine le point $A$ .

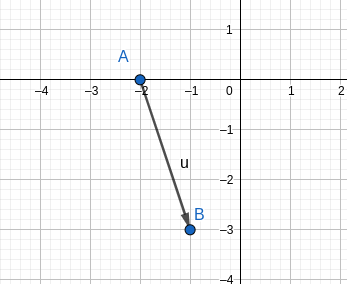
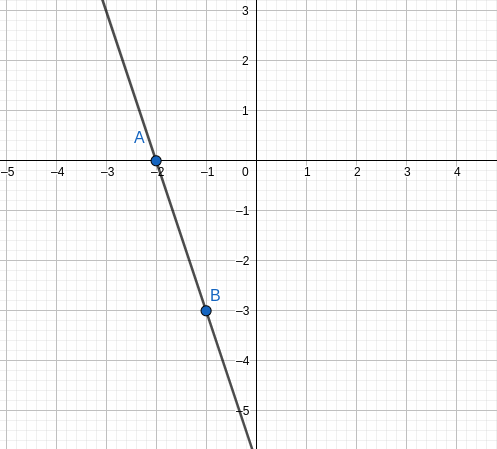
Remarque: l'extrémité du représentant du vecteur dessiné est le point $B(x_A+1~;~y_A+m) = B(-1 ~;~ -3)$ .

D'où une représentation de la droite:

Question☘

Représenter graphiquement la droite de coefficient directeur $-1$ passant par le point $A(-2~;~ 2)$ .

Solution

On commence par placer le point $A$ donné.

La droite ayant un coefficient directeur $m$ est dirigée par le vecteur $\overrightarrow{u}(1~;~m)$ . On représente donc le vecteur $\overrightarrow{u}(1~;~ -1)$ ayant pour origine le point $A$ .

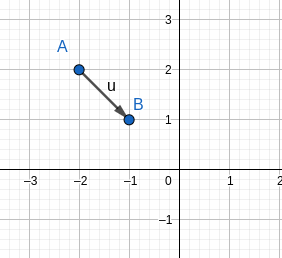
Remarque: l'extrémité du représentant du vecteur dessiné est le point $B(x_A+1~;~y_A+m) = B(-1 ~;~ 1)$ .

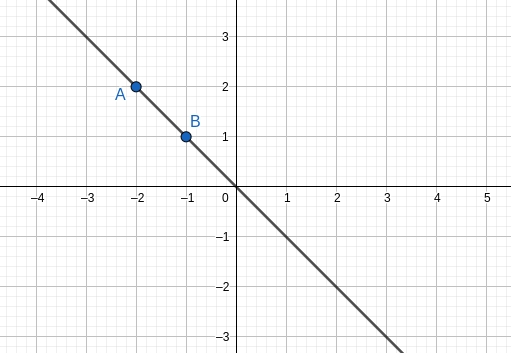
D'où une représentation de la droite:

Question☘

Représenter graphiquement la droite de coefficient directeur $-2$ passant par le point $A(0 ~ ; ~ 1)$ .

Solution

On commence par placer le point $A$ donné.

La droite ayant un coefficient directeur $m$ est dirigée par le vecteur $\overrightarrow{u}(1~;~m)$ . On représente donc le vecteur $\overrightarrow{u}(1~;~ -2)$ ayant pour origine le point $A$ .

L'extrémité du représentant du vecteur $\overrightarrow{u}(1~;~ -2)$ d'origine $A$ est le point $B(x_A+1~;~y_A+m) = B(1 ~;~ -1)$ .

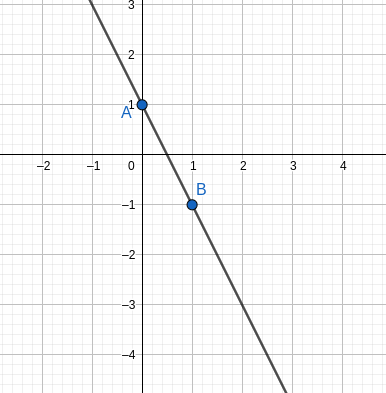
D'où une représentation de la droite:

droite

Question☘

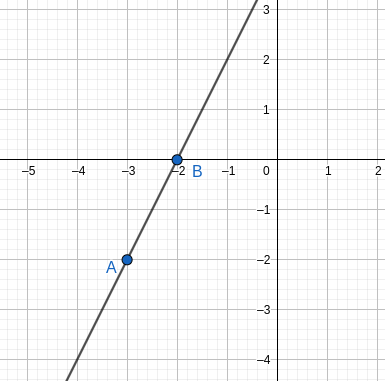
Représenter graphiquement la droite de coefficient directeur $2$ passant par le point $A(-3 ~ ; ~ -2)$ .

Solution

On commence par placer le point $A$ donné.

La droite ayant un coefficient directeur $m$ est dirigée par le vecteur $\overrightarrow{u}(1~;~m)$ . On représente donc le vecteur $\overrightarrow{u}(1~;~ 2)$ ayant pour origine le point $A$ .

L'extrémité du représentant du vecteur $\overrightarrow{u}(1~;~ 2)$ d'origine $A$ est le point $B(x_A+1~;~y_A+m) = B(-2 ~;~ 0)$ .

D'où une représentation de la droite: