Capacité 28☘

Lire graphiquement l’équation réduite d’une droite.

Rappel☘

Pour lire graphiquement l'équation réduite d'une droite:

Si la droite est parallèle à l'axe (Oy) des ordonnées:☘

l'équation est $x = x_A$ (où A est un point quelconque de la droite).

Si la droite est parallèle à l'axe (Ox) des abscisses:☘

l'équation est $y = y_A$ (où A est un point quelconque de la droite).

Sinon (droite "oblique")☘

On lit les coordonnées de deux points de la droite $A(x_A ~;~ y_A)$ et $B(x_B~;~ y_B)$ .

1) On calcule le coefficient directeur $m = \frac{\Delta y}{\Delta x} = \frac{y_B -y_A}{x_B - x_A}$ .

2) L'équation est alors $y = mx+p$ et il nous reste à déterminer $p$ .
Pour cela, on utilise le fait que A est un point de la droite, on doit donc avoir $y_A = mx_A+p$ , la valeur de $p$ est donc obtenue par le calcul: $p = y_A -mx_A$ .

En particulier, lorsque $x_A=0$ , on a $p= y_A$ .

Question☘

On a représenté une droite $d$ sur le graphique ci-après. Déterminer son équation réduite.

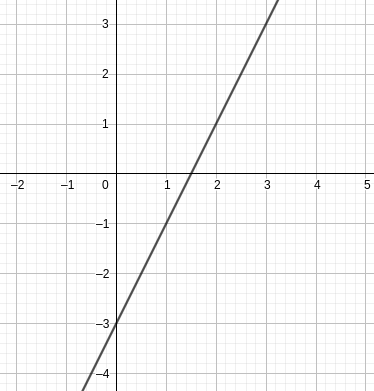
Solution

Les points $A(0;-3)$ et $B(1;-1)$ sont sur la droite.

Le coefficient directeur est $m = \frac{\Delta y}{\Delta x} = 2$ .

Et $A(0;-3)$ est sur la droite, donc $p=-3$ et l'équation est $y = 2x-3$ .

Question☘

On a représenté une droite $d$ sur le graphique ci-après. Déterminer son équation réduite.

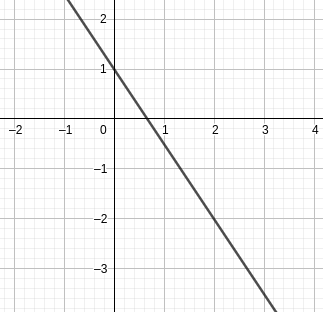
Solution

Les points $A(0;1)$ et $B(2;-2)$ sont sur la droite.

Le coefficient directeur est $m = \frac{\Delta y}{\Delta x} = \frac{-3}{2}$ .

Et $A(0;1)$ est sur la droite, donc $p=1$ et l'équation est $y = \frac{-3}{2}x+1$ .

Question☘

On a représenté une droite $d$ sur le graphique ci-après. Déterminer son équation réduite.

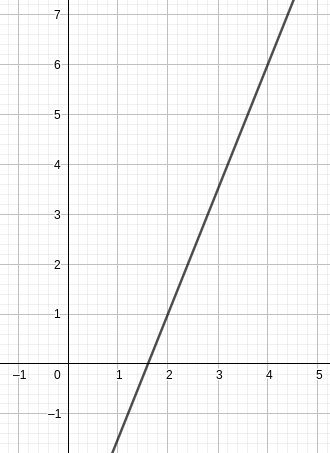
Solution

Les points $A(2;1)$ et $B(4;6)$ sont sur la droite.

Le coefficient directeur est $m = \frac{\Delta y}{\Delta x} = \frac{5}{2}$ .

Et $A(2;1)$ est sur la droite, donc $y_A =\frac{5}{2} x_A +p$ , soit $1 =\frac{5}{2} \times 2 +p$ d'où $p = -4$ .
Et l'équation est $y = \frac{5}{2}x-4$ .

Question☘

On a représenté une droite $d$ sur le graphique ci-après. Déterminer son équation réduite.

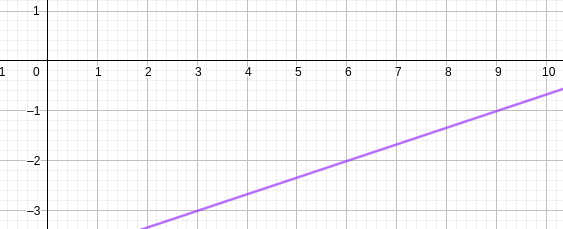
Solution

Les points $A(3;-3)$ et $B(6;-2)$ sont sur la droite.

Le coefficient directeur est $m = \frac{\Delta y}{\Delta x} = \frac{1}{3}$ .

La droite a donc une équation de la forme $y = \frac{1}{3}x+p$ .

Et $A(3;-3)$ est sur la droite, donc $y_A =\frac{1}{3} x_A +p$ , soit $-3 =\frac{1}{3} \times 3 +p$ d'où $p = -4$ .
Et l'équation est $y = \frac{1}{3}x-4$ .

Question☘

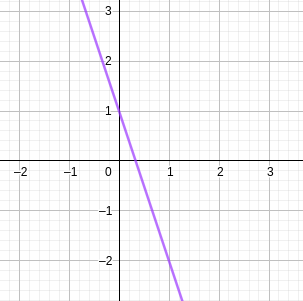
On a représenté une droite $d$ sur le graphique ci-après. Déterminer son équation réduite.

Solution

Les points $A(0;1)$ et $B(1;-2)$ sont sur la droite.

Le coefficient directeur est $m = \frac{\Delta y}{\Delta x} = -3$ .

La droite a donc une équation de la forme $y = -3x+p$ .

Et $A(0;1)$ est sur la droite, donc $p=1$ .
Et l'équation est $y = -3x+1$ .