Capacité 30☘

Déterminer graphiquement le coefficient directeur d’une tangente à une courbe.

Rappels☘

Lien entre coefficient directeur et nombre dérivé☘

Soit $f$ une fonction dérivable en un réel $a$ . Le nombre dérivé $f'(a)$ est le coefficient directeur de la tangente à la courbe représentant $f$ , au point $A(a;f(a))$ .

Lecture graphique d'un coefficient directeur☘

On a dessiné ci-dessous la courbe d'une fonction en vert ainsi que la tangente en un point A (en noir) d'abscisse $a= 6$ .

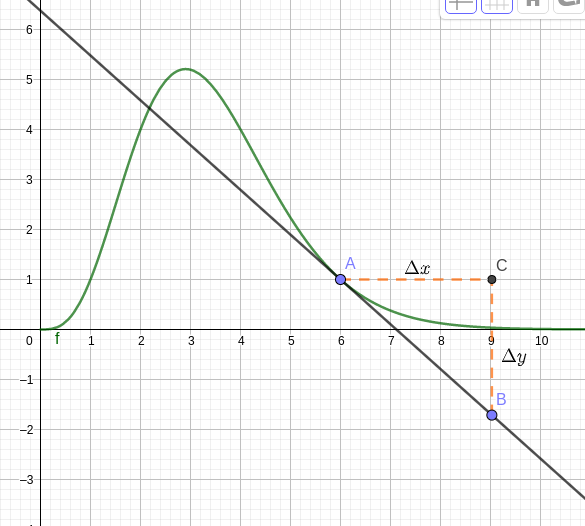
Pour déterminer le nombre dérivé $f'(a)$ , c'est à dire le coefficient directeur de la tangente en A, on peut placer un second point B et calculer $m = \frac{\Delta y}{\Delta x}$ où $\Delta y = y_B - y_A$ et $\Delta x = x_B - x_A$ .

Sur la figure, on a $\Delta y \approx -2,7$ et $\Delta x \approx 3$ , soit $m\approx -0,9$ .

Question☘

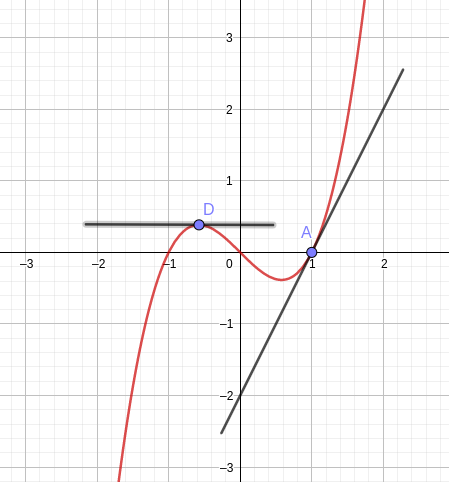
On a dessiné ci-dessous la courbe d'une fonction $f$ et sa tangente au point A d'abscisse 1.

Lire graphiquement le nombre dérivé $f'(1)$ .

Solution

$f'(1)$ est le coefficient directeur de la tangente au point A.

On place un point B sur cette tangente, par exemple $B(2;2)$ et on lit $\Delta y = y_B-y_A = 2$ et $\Delta x = x_B - x_A = 1$ , d'où $f'(1) = 2$ .

Question☘

Sur le graphique de la question précédente, on a aussi représenté une tangente au point D.

Lire graphiquement le coefficient directeur de cette tangente.

Solution

Deux points pris sur cette tangente ont même ordonnée: $\Delta y = 0$ . Le coefficient directeur de la tangente au point D est donc 0.

On a donc $f'(x_D) = 0$ .

Question☘

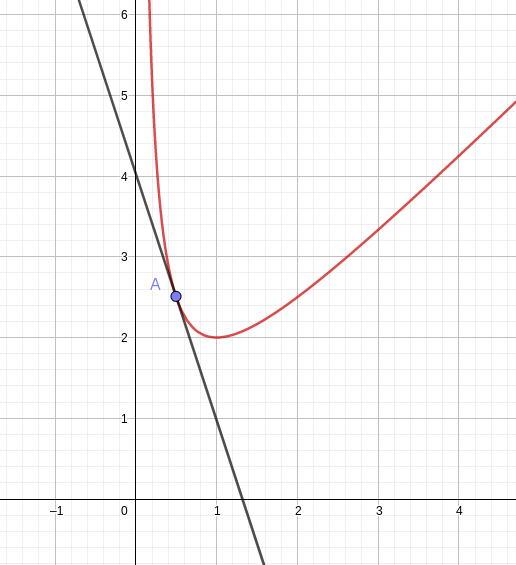
On a dessiné ci-dessous la courbe d'une fonction $f$ et sa tangente au point A d'abscisse 0,5.

Lire graphiquement le nombre dérivé $f'(0,5)$ .

Solution

$f'(0,5)$ est le coefficient directeur de la tangente au point A.

On place un point B sur cette tangente, par exemple $B(0;4)$ et on lit $\Delta y = y_B-y_A = 1,5$ et $\Delta x = x_B - x_A = -0,5$ , d'où $f'(0,5) = -3$ .