Des iris☘

La petite base de données iris est un ensemble de résultats (datant du début du vingtième siècle) très souvent utilisée dans les cours d'initiation à l'intelligence artificielle ou aux statistiques.

Nous allons l'utliser à partir d'un fichier csv (le séparateur pour ce fichier est la virgule).

Contenu du fichier.☘

Les premières lignes:

longueur du sépale	largeur du sépale	espèce
5.1	3.5	Iris-setosa
4.9	3.0	Iris-setosa
4.7	3.2	Iris-setosa
4.6	3.1	Iris-setosa
5.0	3.6	Iris-setosa
5.4	3.9	Iris-setosa
4.6	3.4	Iris-setosa

En colonne 1 on trouve une mesure de la longueur du sépale, en colonne 2 une mesure de sa largeur. Enfin en colonne 3, le type d'iris. Il y a 3 types (ce sera nos "classes"): setosa, versicolor, virginica.

Exercice 1: stockage des données dans une liste.☘

En utilisant la bibliothèque csv, charger le contenu de ce fichier csv dans une liste.

Les éléments de cette liste seront des listes [longueur de sépale, largeur de sépale, classe d'iris].

Un premier code

Commençons par le code suivant (le fichier iris.csv est à placer dans le même dossier que votre fichier python):

import csv

with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')
    # transformation de lecture en liste:
    lecture = list(lecture)

for i in (0,1,2,3):
    print(lecture[i])

On obtient:

['longueur du sépale', 'largeur du sépale', 'espèce']
['5.1', '3.5', 'Iris-setosa']
['4.9', '3.0', 'Iris-setosa']
['4.7', '3.2', 'Iris-setosa']

Nous voyons que la première ligne concerne la légende (et devra donc être éliminée de nos données). Chaque ligne est stockée dans une liste et chaque élément de la ligne a été chargée comme étant une chaîne de caractères. Il nous faut donc transformer largeur et longueur en flottant (avec float).

De chaîne vers flottant

import csv

with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les deux premières données en flottant:
for i, iris in enumerate(lecture):
    lecture[i][0] =  float(iris[0])
    lecture[i][1] =  float(iris[1]) 

# affichage des premières lignes:
for i in (0,1,2,3):
    print(lecture[i])

On obtient:

[5.1, 3.5, 'Iris-setosa']
[4.9, 3.0, 'Iris-setosa']
[4.7, 3.2, 'Iris-setosa']
[4.6, 3.1, 'Iris-setosa']

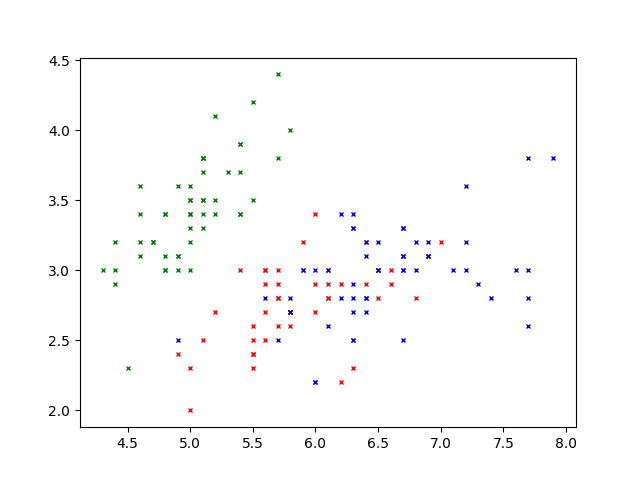
Exercice 2: représentation graphique☘

En vous aidant de ce qui a été fait avec matplotlib.pyplot dans la page sur Voronoï, obtenir la représentation graphique ci-dessous.

Les 3 couleurs correspondent aux 3 classes d'iris (setosa, versicolor, virginica).
L'abscisse est la longueur du sépale.
L'ordonnée est la largeur du sépale.

Code

Un code pour construire cette représentation graphique:

import csv
import matplotlib.pyplot as plt 


with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les deux premières données en flottant:
for i, iris in enumerate(lecture):
    lecture[i][0] =  float(iris[0])
    lecture[i][1] =  float(iris[1])  

# Création des listes des abscisses et ordonnées pour chaque classe:
Xsetosa = [ iris[0] for iris in lecture if iris[2] == 'Iris-setosa' ]
Ysetosa = [ iris[1] for iris in lecture if iris[2] == 'Iris-setosa' ]

Xversicolor = [ iris[0] for iris in lecture if iris[2] == 'Iris-versicolor' ]
Yversicolor = [ iris[1] for iris in lecture if iris[2] == 'Iris-versicolor' ]

Xvirginica = [ iris[0] for iris in lecture if iris[2] == 'Iris-virginica' ]
Yvirginica = [ iris[1] for iris in lecture if iris[2] == 'Iris-virginica' ]

# création du graphique:

plt.plot(Xsetosa,Ysetosa, marker='x', color='g', markersize=3, linestyle='')
plt.plot(Xversicolor,Yversicolor, marker='x', color='r', markersize=3, linestyle='')
plt.plot(Xvirginica,Yvirginica, marker='x', color='b', markersize=3, linestyle='')
plt.show()

Exercice 3☘

La représentation graphique précédente montre que pour une nouvelle fleur à classer parmi les trois espèces, les mesures choisies ne permettent pas une conclusion immédiate (la frontière entre les rouges et les bleus est floue).

On décide d'appliquer le principe de l'algorithme k-NN pour pouvoir classer une nouvelle fleur parmi les trois espèces.

Note

Le botaniste sait les distinguer, il s'agit ici de les classer de façon automatique, c'est la base des algorithmes d'IA (plus spécifiquement du machine learning).

Ce type de classification automatique est la base par exemple de la capacité de votre téléphone à regrouper de façon automatique toutes les photos concernant une même personne.

On commence donc par écrire une fonction prenant en paramètres deux iris (c'est à dire deux éléments de la liste lecture) et renvoyant leur distance mutuelle (où un iris est considéré comme le point de coordonnées (longueur du sépale, largeur du sépale) comme dans le graphique précédent).

Écrire une telle fonction.

def distance(iris1, iris2):
    """
    iris1 -- élément de la liste lecture, forme [float, float, espèce]
    iris2 -- même nature qu'iris1

    renvoie la distance euclidienne entre les deux iris. 
    """

Un code

import csv
from math import sqrt



with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les deux premières données en flottant:
for i, iris in enumerate(lecture):
    lecture[i][0] =  float(iris[0])
    lecture[i][1] =  float(iris[1])  



def distance(iris1, iris2):
    """
    iris1 -- élément de la liste lecture, forme [float, float, espèce]
    iris2 -- même nature qu'iris1

    renvoie la distance euclidienne entre les deux iris
    """
    dx = iris1[0] - iris2[0]
    dy = iris1[1] - iris2[1]
    return sqrt(dx**2 + dy**2)

# exemple (distance entre les deux premiers iris du fichier):
d = distance(lecture[0], lecture[1])
print(d)

Exercice 4☘

Écrire un code possible pour le corps de la fonction suivante:

def kPlusProchesVoisins(iris, k):
    """
    iris -- liste [longueur sépale, largeur sépale] de type [float, float] 
    k -- entier naturel, compris entre 1 et le nombre de données dans le fichier iris.csv

    renvoie la liste des k plus proches voisins 
    (pris dans les données du fichier iris.csv) de iris.

    On rappelle que les données du fichier csv ont été récupérées dans une liste
    nommée lecture.
    """

On utilisera le principe déjà utilisé:

création de la liste des distances de la nouvelle fleur à chacune des fleurs de la base.
Ajout de l'information "indice" (numéro de ligne dans le fichier base) afin que cette information ne soit pas perdue par un tri.
Tri de la liste en ordre croissant des distances.
Récupération des k premiers indices dans la liste ainsi triée.
Et récupération des données correspondantes dans le fichier.

Un code possible

import csv
from math import sqrt



with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les deux premières données en flottant:
for i, iris in enumerate(lecture):
    lecture[i][0] =  float(iris[0])
    lecture[i][1] =  float(iris[1])  



def distance(iris1, iris2):
    """
    iris1 -- élément de la liste lecture, forme [float, float, espèce]
    iris2 -- même nature qu'iris1

    renvoie la distance euclidienne entre les deux iris
    """
    dx = iris1[0] - iris2[0]
    dy = iris1[1] - iris2[1]
    return sqrt(dx**2 + dy**2)



def kPlusProchesVoisins(iris, k):
    """
    iris -- liste [longueur sépale, largeur sépale] de type [float, float] 
    k -- entier naturel, compris entre 1 et le nombre de données dans le fichier iris.csv

    renvoie la liste des k plus proches voisins 
    (pris dans les données du fichier iris.csv) de iris.

    On rappelle que les données du fichier csv ont été récupérées dans une liste
    nommée lecture.
    """
    # on crée la liste des distances entre iris et les données du fichier:
    L = [distance(iris, fleur) for fleur in lecture]
    # on ajoute la donnée "indice":
    M = [(L[i], i) for i in range(len(L))]
    # on trie M suivant les distances, ordre croissant:
    M.sort(key= lambda x: x[0])
    # On récupère uniquement les indices des k premiers éléments:
    I = [ M[i][1] for i in range(k)]
    # on renvoie la liste des fleurs correspondantes:
    return [lecture[k] for k in I]

# exemple:
print(kPlusProchesVoisins([7.3, 2.9], 2))

On obtient:

[[7.3, 2.9, 'Iris-virginica'], [7.2, 3.0, 'Iris-virginica']]

Les deux fleurs issues de notre base de données (fichier iris.csv) qui sont les plus proches (au sens défini ci-dessus) de notre iris de longueur de sépale 7.3 et de largeur de sépale 2.9 sont des virginica.

Avec le critère 2-NN, on décide donc que cette nouvelle fleur est une virginica.

Note

Soulignons une fois de plus que le principe utilisé ici est très simple par rapport aux algorithmes modernes utilisés en IA. Les résultats ne seront sans doute pas bons par rapport à ce que peut obtenir un téléphone récent (il existe des applications de reconnaissance des plantes sur vos smartphones, testez en une à votre prochaine sortie!)

Exercice 5☘

Écrire une fonction python prenant en entrée une nouvelle donnée (et le paramètre k) et donnant en sortie la classe que l'on octroie à cette nouvelle donnée par le principe k-NN.

def classification(iris, k):
    """
    iris -- élément de la forme [float, float]
    k -- k>0

    renvoie l'espèce la plus fréquente 
    parmi les k plus proches voisins de iris 
    """

Un code

import csv
from math import sqrt



with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les deux premières données en flottant:
for i, iris in enumerate(lecture):
    lecture[i][0] =  float(iris[0])
    lecture[i][1] =  float(iris[1])  



def distance(iris1, iris2):
    """
    iris1 -- élément de la liste lecture, forme [float, float, espèce]
    iris2 -- même nature qu'iris1

    renvoie la distance euclidienne entre les deux iris
    """
    dx = iris1[0] - iris2[0]
    dy = iris1[1] - iris2[1]
    return sqrt(dx**2 + dy**2)



def kPlusProchesVoisins(iris, k):
    """
    iris -- liste [longueur sépale, largeur sépale] de type [float, float] 
    k -- entier naturel, compris entre 1 et le nombre de données dans le fichier iris.csv

    renvoie la liste des k plus proches voisins 
    (pris dans les données du fichier iris.csv) de iris.

    On rappelle que les données du fichier csv ont été récupérées dans une liste
    nommée lecture.
    """
    # on crée la liste des distances entre iris et les données du fichier:
    L = [distance(iris, fleur) for fleur in lecture]
    # on ajoute la donnée "indice":
    M = [(L[i], i) for i in range(len(L))]
    # on trie M suivant les distances, ordre croissant:
    M.sort(key= lambda x: x[0])
    # On récupère uniquement les indices des k premiers éléments:
    I = [ M[i][1] for i in range(k)]
    # on renvoie la liste des fleurs correspondantes:
    return [lecture[k] for k in I]


def classification(iris, k):
    """
    iris -- élément de la forme [float, float]
    k -- k>0

    renvoie l'espèce la plus fréquente 
    parmi les k plus proches voisins de iris 
    """

    dico = {'Iris-setosa': 0, 'Iris-versicolor':0, 'Iris-virginica':0}
    # liste des voisins:
    ppv = kPlusProchesVoisins(iris, k)
    # mise à jour compteurs:
    for fleur in ppv:        # fleur de la base: [longueur sépale, largeur, classe]
        dico[fleur[2]] += 1  # fleur[2] est donc la classe (virginica ou setosa ou versicolor)

    # on cherche maintenant le maximum des valeurs du dico:
    maxi = 0
    for espece in dico.keys():
        if dico[espece] > maxi:
            maxi = dico[espece]
            especeDominante = espece

    return especeDominante


# exemple 

## un nouvel iris:
nouvelIris = [5.8, 2.8]
## sa classification en prenant les 3 plus proches voisins:
print(classification(nouvelIris, 3))

Variante

On peut utiliser la fonction max de Python pour rechercher la classe d'iris la plus représentée (modification en fin de fonction classification):

import csv
from math import sqrt



with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les deux premières données en flottant:
for i, iris in enumerate(lecture):
    lecture[i][0] =  float(iris[0])
    lecture[i][1] =  float(iris[1])  



def distance(iris1, iris2):
    """
    iris1 -- élément de la liste lecture, forme [float, float, espèce]
    iris2 -- même nature qu'iris1

    renvoie la distance euclidienne entre les deux iris
    """
    dx = iris1[0] - iris2[0]
    dy = iris1[1] - iris2[1]
    return sqrt(dx**2 + dy**2)



def kPlusProchesVoisins(iris, k):
    """
    iris -- liste [longueur sépale, largeur sépale] de type [float, float] 
    k -- entier naturel, compris entre 1 et le nombre de données dans le fichier iris.csv

    renvoie la liste des k plus proches voisins 
    (pris dans les données du fichier iris.csv) de iris.

    On rappelle que les données du fichier csv ont été récupérées dans une liste
    nommée lecture.
    """
    # on crée la liste des distances entre iris et les données du fichier:
    L = [distance(iris, fleur) for fleur in lecture]
    # on ajoute la donnée "indice":
    M = [(L[i], i) for i in range(len(L))]
    # on trie M suivant les distances, ordre croissant:
    M.sort(key= lambda x: x[0])
    # On récupère uniquement les indices des k premiers éléments:
    I = [ M[i][1] for i in range(k)]
    # on renvoie la liste des fleurs correspondantes:
    return [lecture[k] for k in I]


def classification(iris, k):
    """
    iris -- élément de la forme [float, float]
    k -- k>0

    renvoie l'espèce la plus fréquente 
    parmi les k plus proches voisins de iris 
    """
    dico = {'Iris-setosa': 0, 'Iris-versicolor':0, 'Iris-virginica':0}
    # liste des voisins:
    ppv = kPlusProchesVoisins(iris, k)
    # mise à jour compteurs:
    for fleur in ppv:        # fleur de la base: [longueur sépale, largeur, classe]
        dico[fleur[2]] += 1  # fleur[2] est donc la classe (virginica ou setosa ou versicolor)

    # on cherche maintenant le maximum des valeurs du dico:
    effectifs_classe = [(clef, valeur) for clef, valeur in dico.items()]
    maxi = max(effectifs_classe, key= lambda x: x[1])
    return maxi[0]


# exemple 

## un nouvel iris:
nouvelIris = [5.8, 2.8]
## sa classification en prenant les 3 plus proches voisins:
print(classification(nouvelIris, 3))

Exemple avec représentation graphique

L'exemple d'utilisation suivant (avec graphique):

import csv
from math import sqrt



with open('iris.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les deux premières données en flottant:
for i, iris in enumerate(lecture):
    lecture[i][0] =  float(iris[0])
    lecture[i][1] =  float(iris[1])  



def distance(iris1, iris2):
    """
    iris1 -- élément de la liste lecture, forme [float, float, espèce]
    iris2 -- même nature qu'iris1

    renvoie la distance euclidienne entre les deux iris
    """
    dx = iris1[0] - iris2[0]
    dy = iris1[1] - iris2[1]
    return sqrt(dx**2 + dy**2)



def kPlusProchesVoisins(iris, k):
    """
    iris -- liste [longueur sépale, largeur sépale] de type [float, float] 
    k -- entier naturel, compris entre 1 et le nombre de données dans le fichier iris.csv

    renvoie la liste des k plus proches voisins 
    (pris dans les données du fichier iris.csv) de iris.

    On rappelle que les données du fichier csv ont été récupérées dans une liste
    nommée lecture.
    """
    # on crée la liste des distances entre iris et les données du fichier:
    L = [distance(iris, fleur) for fleur in lecture]
    # on ajoute la donnée "indice":
    M = [(L[i], i) for i in range(len(L))]
    # on trie M suivant les distances, ordre croissant:
    M.sort(key= lambda x: x[0])
    # On récupère uniquement les indices des k premiers éléments:
    I = [ M[i][1] for i in range(k)]
    # on renvoie la liste des fleurs correspondantes:
    return [lecture[k] for k in I]


def classification(iris, k):
    """
    iris -- élément de la forme [float, float]
    k -- k>0

    renvoie l'espèce la plus fréquente 
    parmi les k plus proches voisins de iris 
    """

    dico = {'Iris-setosa': 0, 'Iris-versicolor':0, 'Iris-virginica':0}
    # liste des voisins:
    ppv = kPlusProchesVoisins(iris, k)
    # mise à jour compteurs:
    for fleur in ppv:        # fleur de la base: [longueur sépale, largeur, classe]
        dico[fleur[2]] += 1  # fleur[2] est donc la classe (virginica ou setosa ou versicolor)

    # on cherche maintenant le maximum des valeurs du dico:
    effectifs_classe = [(clef, valeur) for clef, valeur in dico.items()]
    maxi = max(effectifs_classe, key= lambda x: x[1])
    return maxi[0]



if __name__ == '__main__':

    import matplotlib.pyplot as plt

    nouvelIris = [5.8, 2.8]
    k = 3
    ppv = kPlusProchesVoisins(nouvelIris, k)
    print(ppv)
    print(classification(nouvelIris, k))


    # Création des listes des abscisses et ordonnées pour chaque classe:
    Xsetosa = [ iris[0] for iris in lecture if iris[2] == 'Iris-setosa' ]
    Ysetosa = [ iris[1] for iris in lecture if iris[2] == 'Iris-setosa' ]

    Xversicolor = [ iris[0] for iris in lecture if iris[2] == 'Iris-versicolor' ]
    Yversicolor = [ iris[1] for iris in lecture if iris[2] == 'Iris-versicolor' ]

    Xvirginica = [ iris[0] for iris in lecture if iris[2] == 'Iris-virginica' ]
    Yvirginica = [ iris[1] for iris in lecture if iris[2] == 'Iris-virginica' ]

    Xppv = [ iris[0] for iris in ppv ]
    Yppv = [ iris[1] for iris in ppv ]


    # création du graphique:

    plt.plot(Xsetosa,Ysetosa, marker='D', color='g', markersize=6, linestyle='')
    plt.plot(Xversicolor,Yversicolor, marker='D', color='r', markersize=6, linestyle='')
    plt.plot(Xvirginica,Yvirginica, marker='D', color='b', markersize=6, linestyle='')
    plt.plot(Xppv,Yppv, marker='+', color='k', markersize=6, linestyle='')
    plt.plot(nouvelIris[0], nouvelIris[1], marker='o', color='y', markersize=4)
    plt.show()

donne:

[[5.8, 2.8, 'Iris-virginica'], [5.7, 2.8, 'Iris-versicolor'], [5.8, 2.7, 'Iris-versicolor']]
Iris-versicolor

permet de voir qu'avec k = 1 la conclusion serait virginica mais qu'elle est versicolor avec k = 3.

En fait, avec k = 3, la conclusion pourrait être également virginica: lorsqu'on consulte le fichier csv, on constate qu'il y a également un iris (5.8, 2.7) de type virginica. L'algorithme aurait pu choisir cet iris plutôt que le versicolor de mêmes caractéristiques.

Ce qui résulte de cette remarque est que le procédé semble peu fiable. C'est pourquoi on complète en général l'implémentation de l'algorithme par des tests de fiabilité à l'aide de données sur lesquelles on connaît la réponse. Pour une grande fiabilité, la taille de la base de données et le choix de k sont deux clefs importantes.

Exercice 6☘

En fait, la base de données iris est un peu plus complète et comporte également largeur et longueur des pétales.

Chargez le fichier complet puis modifiez le script précédent pour tenir compte de ces mesures supplémentaires.

Efforcez vous d'apporter des modifications "durables" au sens où on aimerait minimiser le nombre de modifications à apporter au code en cas de nouvel ajout de mesures dans les lignes de données.

Note

Si la taille de la base de données et le choix de k sont deux clefs importantes pour la fiabilité de prédiction, le nombre et le choix des attributs qui vont alimenter la base jouent évidemment également un rôle crucial.

Aide

Il s'agit essentiellement de modifier la fonction distance qui doit maintenant tenir compte du fait que l'on a 4 données par fleur. On calculera la distance avec la même formule mais avec quatre termes sous la racine (c'est la distance euclidienne entre deux points dans un espace de dimension 4).

Distance( A(x,y,z,t), B(a,b,c,d) ) = $\sqrt{(x-a)^2 + (y-b)^2 + (z-c)^2 + (t-d)^2}$ .

Un code

import csv
from math import sqrt


# nom du fichier de données
# défini ici en constante préalable afin que toute modification ultérieure
# puisse autant que possible se limiter aux premières lignes de ce code
BASE_DE_DONNEES = 'irisComplet'

# on définit une constante correspondant au nombre de données  (nombre de mesures)
# dans chaque ligne
# On s'évertue à écrire un code pour lequel seule cette constante
# sera à modifier si on ajoute encore des mesures à la base
NB_DONNEES = 4

with open(BASE_DE_DONNEES + '.csv', newline='') as fichierIris:
    lecture = csv.reader(fichierIris, delimiter=',')    
    # transformation de lecture en liste:
    lecture = list(lecture)


# on élimine la ligne de légende:
lecture.pop(0) 
# on transforme les NB_DONNEES premières données en flottant:
for i in range(len(lecture)): 
    for j  in range(NB_DONNEES):
        lecture[i][j] =  float(lecture[i][j])





def distance(iris1, iris2):
    """
    iris1 -- élément de la forme liste de NB_DONNEES flottants
    iris2 -- même nature qu'iris1 ou liste
    de NB_DONNEES flottants suivis de la chaîne donnant l'espèce.

    renvoie la distance euclidienne entre les deux iris
    """
    # les écarts sur chaque coordonnée:
    ecarts = [iris1[j] - iris2[j] for j in range(NB_DONNEES)]
    # somme des carrés des écarts:
    sommeCarresEcarts = sum([ecart**2 for ecart in ecarts])
    return sqrt(sommeCarresEcarts)






def kPlusProchesVoisins(iris, k):
    """
    iris -- liste [longueur sépale, largeur sépale] de type [float, float, float, float] 
    k -- entier naturel, compris entre 1 et le nombre de données dans le fichier iris.csv

    renvoie la liste des k plus proches voisins 
    (pris dans les données du fichier iris.csv) de iris.

    On rappelle que les données du fichier csv ont été récupérées dans une liste
    nommée lecture.
    """
    # on crée la liste des distances entre iris et les données du fichier:
    L = [distance(iris, fleur) for fleur in lecture]
    # on ajoute la donnée "indice":
    M = [(L[i], i) for i in range(len(L))]
    # on trie M suivant les distances, ordre croissant:
    M.sort(key= lambda x: x[0])
    # On récupère uniquement les indices des k premiers éléments:
    I = [ M[i][1] for i in range(k)]
    # on renvoie la liste des fleurs correspondantes:
    return [lecture[k] for k in I]


def classification(iris, k):
    """
    iris -- élément de la forme [float, float]
    k -- k>0

    renvoie l'espèce la plus fréquente 
    parmi les k plus proches voisins de iris 
    """

    dico = {'Iris-setosa': 0, 'Iris-versicolor':0, 'Iris-virginica':0}
    # liste des voisins:
    ppv = kPlusProchesVoisins(iris, k)
    # mise à jour compteurs:
    for fleur in ppv:         
        dico[fleur[-1]] += 1  # fleur[-1] est  la classe (virginica ou setosa ou versicolor)

    # on cherche maintenant le maximum des valeurs du dico:
    effectifs_classe = [(clef, valeur) for clef, valeur in dico.items()]
    maxi = max(effectifs_classe, key= lambda x: x[1])
    return maxi[0]



if __name__ == '__main__':        
    nouvelIris = [4.6, 3.6, 1.0, 0.2]
    k = 3
    ppv = kPlusProchesVoisins(nouvelIris, k)
    print(ppv)
    print(classification(nouvelIris, k))