Le type int

Objet et type

Toutes les "valeurs" que l'on manipulera en python sont des "objets" ayant un "type".

Pour connaître le type d'un objet, on utilisera la fonction type:

>>> type(3)
<class 'int'>
>>> type(3.0)
<class 'float'>

int est le type correspondant aux entiers (int est l'abréviation de integer).

float est le type correspondant aux décimaux (float se traduit en français par flottant. Vous pourrez retenir pour le moment qu'il s'agit des nombres avec une partie décimale présente explicitement comme 4.5, 3.14 ou encore 5.0).

Le type entier

Les entiers en langage python sont représentés par des objets de type int.

Info

int est l'abréviation de integer qui signifie entier.

Opérations sur les entiers.

On peut ajouter des entiers, soustraire des entiers, multiplier des entiers entre eux: le résultat sera toujours un entier.

>>> type(2+3)
<class 'int'>
>>> type(3*4)
<class 'int'>
>>> type(3-7)
<class 'int'>

Puissance

a et b étant deux entiers, $a^b$ s'obtient avec **:

>>> 2**3
8
>>> type(4**2)
<class 'int'>

Division

Un réel non entier

Si l'on divise 5 par 2, on obtient $2{,}5$: ce n'est pas un entier. Cela se confirme avec python, heureusement:

>>> 5/2
2.5
>>> type(5/2)
<class 'float'>

Info

float se traduit par flottant. Un flottant représente un nombre décimal.

Un réel entier

Si l'on divise 12 par 4, on obtient 3, n'est-ce pas? Donc $\frac{12}{4}$ est un entier.

Qu'en dit python?

>>> type(12/4)
<class 'float'>

Et si l'on demande explicitement le résultat:

>>> C
3.0

On obtient un flottant et non un int. Pourtant ici, on avait bien au départ deux int...

Explication: / est l'opération de division définie sur les flottants. 12/4 est donc réinterprété comme étant 12.0/4.0 et fournira un flottant.

Attention: le nombre $3{,}0$ est, mathématiquement, un entier. Mais informatiquement, ce flottant n'est pas un int. En effet, les entiers et les flottants ne sont pas du tout codés de la même façon en machine et cette différence de codage entraînera des différences de "comportement" vis-à-vis des opérations. Veillez donc bien toujours à faire la distinction entre le nombre mathématique et l'objet codé en machine.

Attention

3 et 3.0 représentent en mathématiques le même nombre. Mais dans les langages de programmation, il s'agit de deux objets de types différents.

Notamment l'opération 3+3 et l'opération 3.0+3.0 par exemple s'exécutent avec des algorithmes différents. Les opérations sur un type d'objet se programment en effet en général avec le reste du programme définissant cet objet. L'addition des entiers, l'addition des flottants sont donc deux additions différentes: elles agissent sur des objets qui sont codés différemment, utiliser le même programme pour ces deux additions est donc tout simplement impossible.

Exemple de différence de comportement entre 2 et 2.0

Supposons que l'on veuille connaître le nombre d' adresses IPv6 possibles. Une adresse IPv6 est codée sur 128 bits, le nombre d'adresses possibles est donc $2^{128}$.

Effectuons le calcul avec python:

>>> 2**128
340282366920938463463374607431768211456
>>> 2.0**128
3.402823669209385e+38

Le calcul est exact si l'on calcule en utilisant un entier (2) et il n'est pas exact si l'on utilise un flottant (2.0). On constate là des différences de comportement qu'il faudra bien avoir en tête lorsqu'on code.

Division entière

La division entière (ou division euclidienne) de deux entiers produit deux entiers: le quotient et le reste.

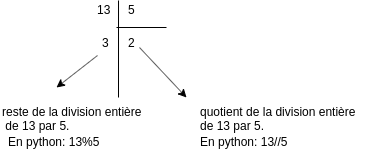
En langage python, le reste est obtenu avec % et le quotient avec //.

>>> 13%5
3
>>> 13//5
2
>>> type(13%5)
<class 'int'>
>>> type(13//5)
<class 'int'>

Info

% est souvent nommé opérateur modulo. a et b étant deux entiers, plutôt que de lire "a%b" sous la forme "reste de a divisé par b", on lira en général "a modulo b".