QCM☘

Note

Les QCM sont là pour vous aider à contrôler ce que vous avez retenu. Si vous ne répondez pas à toutes les questions sans hésitation, c'est sans doute qu'il faut refaire des lectures des pages précédentes.

Trouvez la ou les bonnes réponses.

QCM 1☘

Dans l'interpréteur python:

>>> 3 + 2.0

J'obtiens une erreur " TypeError: unsupported operand type(s) for +: 'int' and 'float' ".
J'obtiens 5.0.
Le résultat est de type int.
Le résultat est de type float.

Réponse

J'obtiens une erreur " TypeError: unsupported operand type(s) for +: 'int' and 'float' ".
J'obtiens 5.0.
Le résultat est de type int.
Le résultat est de type float.

Rappelons en effet que lorsqu'on propose à Python une opération entre un int et un float, Python commence par transformer l'objet de type int en un objet de type float qui lui est proche puis effectue l'algorithme concernant l'opération entre flottants.

QCM 2☘

Dans l'interpréteur python:

>>> 3 + 12/4

J'obtiens 6.
J'obtiens 6.0.
Le résultat est de type int.
Le résultat est de type float.

Réponse

L'opérateur / donne toujours un float et pour additionner un int (ici 3) et un float (3.0 = 12/4), python transforme d'abord l'objet de type int en un objet de type float puis ajoute les float.

J'obtiens 6.
J'obtiens 6.0.
Le résultat est de type int.
Le résultat est de type float.

QCM 3☘

Dans l'interpréteur python:

>>> 2//3

J'obtiens 0.
J'obtiens 0.6666666666666666.
Le résultat est de type int.
Le résultat est de type float.

Réponse

2//3 est le quotient de la division entière de 2 par 3: $2 = 3\times 0 + 2$ .

J'obtiens 0.
J'obtiens 0.6666666666666666.
Le résultat est de type int.
Le résultat est de type float.

QCM 4☘

Dans l'interpréteur python:

>>> 2**3

Réponse

2**3 = $2^3$ = $2\times 2 \times 2$ = 8.

QCM 5☘

Dans l'interpréteur python:

>>> 2**3.0

J'obtiens une erreur.
J'obtiens 8.
J'obtiens 8.0.
J'obtiens 9.0.

Réponse

2**3.0 est réinterprété comme étant 2.0**3.0.

J'obtiens une erreur.
J'obtiens 8.
J'obtiens 8.0.
J'obtiens 9.0.

QCM 6☘

Une adresse IPv6 est codée sur 128 bits. Il y en a donc a priori:

$2^{128}$
$128^2$
$128 \times 2$
$128$

Réponse

$2^{128}$
$128^2$
$128 \times 2$
$128$

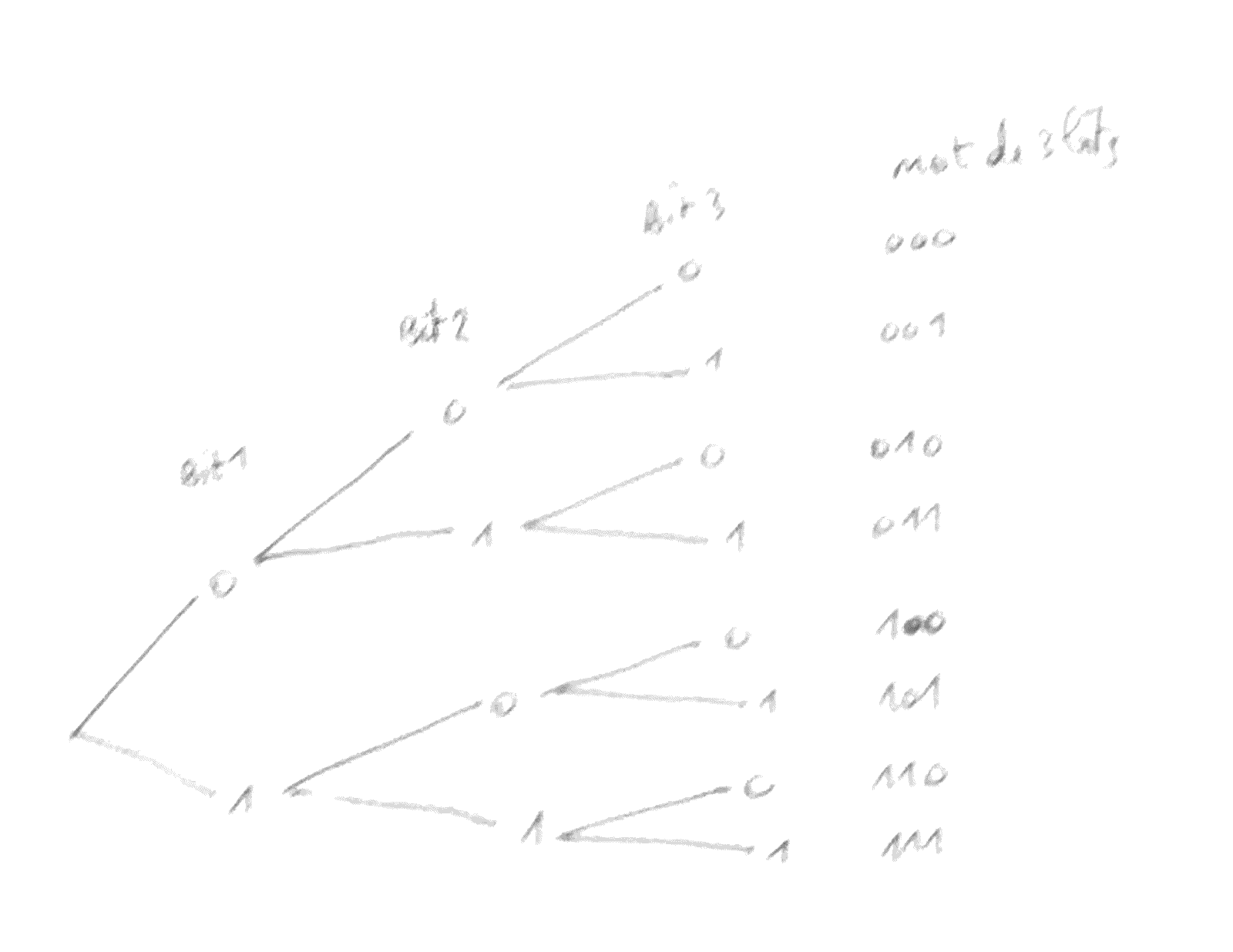
Il y en a $2^{128}\approx 3{,}4\cdot 10^{38}$ car un bit peut avoir deux valeurs (0 ou 1).

Pour se souvenir de ceci, il faut retrouver le résultat en commençant un arbre de dénombrement. Par exemple avec des mots de longueur 3 bits, l'arbre ci-dessous montre que l'on peut écrire $2\times 2 \times 2 = 2^3$ mots.

QCM 7☘

J'entre dans l'interpréteur python:

>>> 13//3, 13%3

J'obtiens (4, 1).
J'obtiens (1, 4).
J'obtiens (4.0, 1).
J'obtiens (4.333333333333333, 1).

Réponse

J'obtiens (4, 1), c'est à dire le couple (quotient de la division entière de 13 par 3, reste de la division entière de 13 par 3).

J'obtiens (4, 1).
J'obtiens (1, 4).
J'obtiens (4.0, 1).
J'obtiens (4.333333333333333, 1).

Nous verrons pourquoi python ajoute des parenthèses: il s'agit en fait d'un objet de type tuple. Un tuple avec deux composantes comme ici est ce que l'on appelle en mathématiques un couple (c'est ce que l'on utilise par exemple pour parler du couple des coordonnées d'un point dans un repère).

QCM 8☘

Je veux avoir la valeur exacte de $2^{128}$ . Dans l'interpréteur python, j'entre:

2.0**128
2**128
2.0^128
2^128

Réponse

La réponse est 2**128. La réponse 1 correspond à un calcul avec des flottants: la valeur ne sera pas exacte. Les réponses 3 et 4 ne conviennent pas car ^ ne correspond pas à un exposant en langage python mais à un autre type de calcul.

2.0**128
2**128
2.0^128
2^128

QCM 9☘

Dans un programme python, des calculs complexes ont mené à deux résultats a et b de type float. On aimerait savoir si a et b sont égaux.

On utilise:

a == b

>>> from math import isclose
>>> isclose(a,b)

On ne peut pas savoir si a et b sont égaux.

Réponse

La question présente une certaine ambiguité:

est ce qu'on veut savoir si les objets python de type float sont égaux ? Dans ce cas a==b convient.
ou est ce qu'on veut savoir si les nombres réels représentés par ces flottants sont égaux ? Dans ce cas, on ne peut pas vraiment savoir. a==b est à éviter comme on l'a déjà souligné et isclose permet de savoir si les flottants obtenus sont très proches ou non mais ne permettra pas de conclure de façon certaine à l'égalité des nombres réels représentés par a et b..

On ne vous posera pas en NSI de questions subtiles sur le sujet: ce qu'il faut retenir, c'est que l'usage de == sur des flottants n'apporte pas de renseignement intéressant en général sur les nombres qu'ils sont censés représenter et ne devra donc pas être utilisé.

QCM 10☘

Dans un interpréteur python:

>>> for i in range(1,10):
...     for j in range(1,10):
...             for k in range(1,10):
...                     if (i/10+j/10)+k/10 != i/10+(j/10+k/10):
...                             print(i,j,k)

Je n'obtiens aucun affichage.
Tous les triplets (i, j, k) sont affichés (avec $1 \leqslant i \leqslant 9$ ; $1 \leqslant j \leqslant 9$ ; $1 \leqslant k \leqslant 9$ ).
Certains triplets (i, j, k) sont affichés (mais pas tous).

Rappel sur !=

!= est utilisé pour tester si deux objets python sont différents.

>>> 2 != 3
True
>>> 2 != 2
False

Nous verrons toutefois qu'il faut être prudent sur son usage, d'une part sur des objets de type plus complexe (voir plus tard dans l'année pour ce problème), mais d'autre part également pour des situations simples:

>>> 2 != 2.0
False
>>> 2 == 2.0
True

On pourrait s'attendre à avoir la réponse False pour 2 == 2.0 puisque les objets 2 et 2.0 ne sont pas de même type.
On devrait plutôt s'attendre à une erreur puisqu'on cherche à comparer des objets qui ne sont pas de même type, ce qui n'a pas de sens a priori. C'est d'ailleurs ce qu'il se passe avec certains langages de programmation.
En python, on applique la remarque déjà faite: l'objet de type int est d'abord transformé en objet de type float puis la comparaison est en fait évaluée entre les objets 2.0 et 2.0. On obtient ici True.
En fait, dans la pratique, vous ne devrez jamais utiliser un tel test avec un flottant: nous avons déjà signalé que l'utilisation de == (et donc de !=) entre flottants est à exlcure.

Réponse

Je n'obtiens aucun affichage.
Tous les triplets (i, j, k) sont affichés.
Certains triplets (i, j, k) sont affichés (mais pas tous).

On a vu en effet dans le cours:

>>> (0.3+0.9)+0.2==0.3+(0.9+0.2)
False

ce qui s'écrit aussi

>>> (3/10+9/10)+2/10 == 3/10+(9/10+2/10)
False

Le triplet (i, j, k) = (3, 9, 2) sera donc affiché. Mais les triplets ne sont pas tous affichés.

Par exemple le triplet (1, 1, 1) ne sera pas affiché:

>>> (1/10 + 1/10) + 1/10 == 1/10 + (1/10+ 1/10)
True

Encore une fois, un tel test avec des flottants est à proscrire. Il pourrait toutefois servir, comme dans cet exemple, à "étudier" l'arithmétique des flottants (ce que nous ne ferons pas en NSI, ce problème est trop technique).