Additionneurs☘
En combinant les portes logiques, on obtient des circuits plus complexes. Notamment le circuit additionneur, circuit fondamental, qui permet d'additionner deux entiers (en binaire bien entendu).
Demi-Additionneur☘
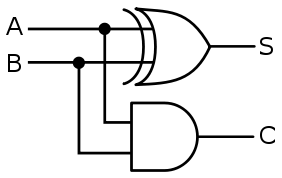
- Le demi-additionneur est un circuit combinatoire qui permet de réaliser la somme arithmétique de deux entiers valant 0 ou 1.
- En sortie, on obtient le bit S de l'unité de la somme et le bit C de la retenue (carry en anglais).
Note
Ceci a déjà été vu dans le cours sur les booléens.
Révisez!
Exercice☘
- Nommer les deux portes logiques du demi-additionneur ci-dessus.
- Construire la table de vérité du demi additionneur.
| A | B | S (bit unité de la somme) | C (bit de retenue) |
|---|---|---|---|
| 0 | 0 | ||
| 0 | 1 | ||
| 1 | 0 | ||
| 1 | 1 |
Solution
La porte XOR donne le bit unité.
La porte AND donne le bit de retenue.
| A | B | S | C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Additionneur☘
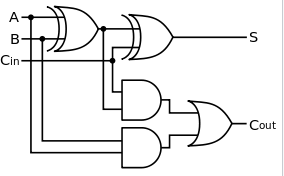
En combinant deux portes "OU EXCLUSIF", deux portes "ET" et une porte "OU", on obtient un additionneur.
Comme son nom l'indique, l'additionneur permet d'additionner 2 bits (E1 et E2) en tenant compte de la retenue entrante ("Cin" "carry in" en anglais). En sortie on obtient le bit de l'unité du résultat de l'addition (S) et la retenue sortante ("Cout").
Exercice☘
Établir la table de vérité de l'additionneur
| A | B | Cin | Cout | S |
|---|---|---|---|---|
| 0 | 0 | 0 | ||
| 0 | 0 | 1 | ||
| 0 | 1 | 0 | ||
| 0 | 1 | 1 | ||
| 1 | 0 | 0 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 0 | ||
| 1 | 1 | 1 |
Solution
| A | B | Cin | Cout | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Remarque
En combinant plusieurs circuits "additionneur", on obtient des additionneurs capables d'additionner des nombres codés sur plusieurs bits.