Les circuits logiques☘
Note
On introduit les circuits logiques, éléments essentiels des machines actuelles. On détaillera un peu plus ces circuits logiques dans le cours suivant.
Un circuit logique permet de réaliser une opération booléenne.
Note
Georges Boole: mathématicien britanique, 1815-1864.
Un circuit logique prend en entrée un ou des signaux électriques. Chaque entrée est
- dans un état "haut" (symbolisé par 1)
- ou dans un état "bas" (symbolisé par 0)
Un circuit logique donne en sortie un ou des signaux électriques (chaque sortie est aussi dans un état "haut" ou à un état "bas").
La porte NON☘
Le plus simple des circuits combinatoires est la porte "NON" (NOT) qui inverse l'état de l'entrée:
| Entrée | Sortie |
|---|---|
| 1 | 0 |
| 0 | 1 |
Schéma usuel de la porte NON:

La porte OU☘
La porte "OU" (OR) a deux entrées (E1, E2) et une sortie S:

| E1 | E2 | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
La porte ET☘
La porte "ET" (AND) a deux entrées (E1, E2) et une sortie S:
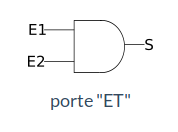
| E1 | E2 | S |
|---|---|---|
| 0 | O | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
La porte OU EXCLUSIF☘
La porte "OU EXCLUSIF" (XOR) a deux entrées (E1, E2) et une sortie S:
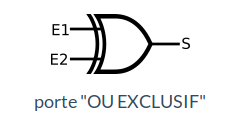
| E1 | E2 | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Remarque
En combinant les portes logiques ET, OU, NON, on obtient tous les circuits complexes nécessaires.
L'exemple de l'additionneur est donné en page suivante.