De la base 10 vers la base b

Comment obtenir les chiffres binaires d'un réel positif?

Les chiffres en base 10

Comment obtenir séquentiellement les chiffres de 8643,5712?

Les chiffres de la partie entière

On a déjà rappelé comment on obtient de façon séquentielle les chiffres de la partie entière par une succession de divisions par 10 (divisions en cascade):

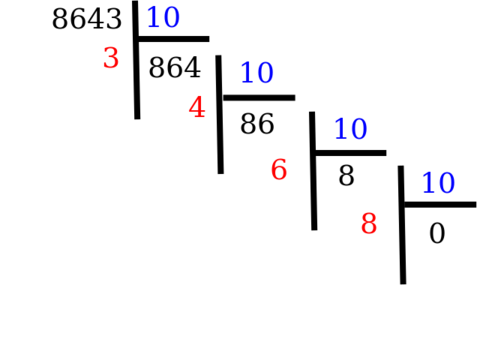
Les chiffres de la partie décimale

De façon analogue, les chiffres de la partie décimale s'obtiennent par une succession de multiplications par 10: on isole la partie entière à chaque étape (c'est le chiffre suivant) et on multiplie par 10 la partie décimale (nombre de la forme 0,...).
Lorsque le "reste décimal" vaut 0, on stoppe.

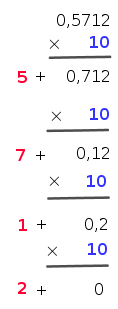
ou encore (en ligne):

• 0,5712 × 10 = 5 + 0,712
• 0,712 × 10 = 7 + 0,12
• 0,12 × 10 = 1 + 0,2
• 0,2 × 10 = 2 + 0,0

Les chiffres sont 5, 7, 1, 2.

Important

Les chiffres de la partie décimale sont obtenus dans l'ordre d'écriture usuelle lors des multiplications succesives.
Les chiffres de la partie entière sont obtenus "à contre-sens" de l'écriture usuelle lors des divisions successives.

En résumé, dans les deux cas, les chiffres s'obtiennent à partir de la virgule (donc de gauche à droite pour les chiffres de la partie entière et de droite à gauche pour les chiffres de la partie décimale).

Les chiffres en base 2

On procède de la même façon.

Soit x un réel positif.

• Les chiffres binaires de la partie entière de x s'obtiennent par des divisions successives (divisions en cascade) par 2 (on obtient en premier celui qui est le plus près de la virgule, c'est à dire l'unité).
• Les chiffres binaires de la partie décimale s'obtiennent par des multiplications successives par 2 (on obtient en premier celui qui est le plus près de la virgule, c'est à dire le coefficient de $\frac{1}{2}$).

Chiffres binaires de 3,25.

• On écrit d'abord 3 en binaire comme on a déjà appris à le faire: 3 = 11₂.
• On écrit ensuite 0,25 en binaire par des multiplications successives par 2:
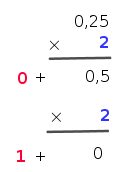  On a donc 0,25 = 0,01₂

D'où 3,25 = 11,01₂.

Chiffres binaires de 5,625

• On écrit la partie entière en binaire: 5 = 101₂
• On écrit ensuite la partie décimale en binaire:
  • 0,625 × 2 = 1,25 = 1 + 0,25
  • 0,25 × 2 = 0,5 = 0 + 0,5
  • 0,5 × 2 = 1 = 1 + 0,0
    On a donc 0,625 = 0,101₂

Et 5,625 = 101,101₂.

Exercice

Donner l'écriture binaire des nombres suivants:

• a = 7,125

a

• 7 = 111₂
• Partie décimale:
  • 0,125 × 2 = 0,25 = 0 + 0,25
  • 0,25 × 2 = 0,5 = 0 + 0,5
  • 0,5 × 2 = 1 = 1 + 0,0

Donc 0,125 = 0,001₂ et 7,125 = 111,001₂.

• b = 13,0625

b

• 13 = 1101₂
• Partie décimale:
  • 0,0625 × 2 = 0,125 = 0 + 0,125
  • 0,125 × 2 = 0,25 = 0 + 0,25
  • 0,25 × 2 = 0,5 = 0 + 0,5
  • 0,5 × 2 = 1 = 1 + 0,0

Donc 0,0625 = 0,0001₂ et 13,0625 = 1101,0001₂

• c = 4,75

c

• 4 = 100₂
• Partie décimale:
  • 0,75 × 2 = 1,5 = 1 + 0,5
  • 0,5 × 2 = 1 = 1 + 0,0

Donc 0,75 = 0,11₂ et 4,75 = 100,11₂.

Un convertisseur en ligne

Vous pouvez créer vous-même d'autres exercices pour vous entraîner et vérifier vos calculs avec un convertisseur.
Par exemple, ce convertisseur en ligne.