Complément à deux et cercle☘

Les entiers sur un cercle☘

les positifs☘

Nous avons vu précédemment qu'en complément à deux sur 8 bits, les codes ayant un 0 à gauche désignent les positifs:

0000 0000 représente 0,
0000 0001 représente 1,
0000 00010 représente 2,
0000 0011 représente 3,
0000 0100 représente 4,
...,
0111 1111 représente 127

Il s'agit de l'écriture usuelle en base deux de ces entiers.

les négatifs☘

Les codes ayant un 1 à gauche désignent les négatifs. le bit la plus à gauche peut donc être lu comme un bit de signe:

0 à gauche: signe +.
1 à gauche: signe -.

Par contre, les 7 bits qui suivent ne sont pas à lire comme l'écriture en base deux des valeurs absolues dans le cas d'un négatif mais comme celle du complément à deux de leur valeur absolue.

Une présentation sur un cercle☘

L'idée est la suivante:
après le code 0111 1111 qui désigne +127 (le dernier positif), on repart à -128:

1000 0000 représente -128,
1000 0001 représente -127,
1000 0010 représente -126,
...
1111 1111 représente -1.

Pour avoir une image de ce choix, vous pouvez imaginer que l'on tourne sur un cercle: dans un sens, on compte en positif les pas, dans l'autre sens on les compte en négatif. En complément à 2 sur 8 bits, on découpe en 2⁸ = 256 arcs de même longueur.

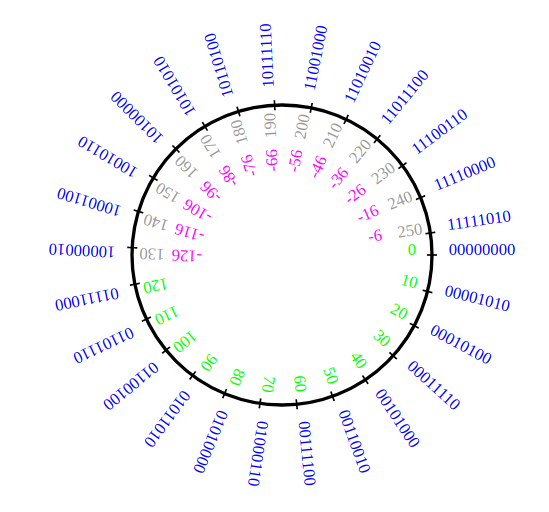
On voit sur cette image que -1 va correspondre à 255 (on fait un pas dans le sens négatif à partir de 0) et sera donc codé par l'écriture binaire de 255, c'est à dire par $1111\ 1111$ .

Si on pense "en tour", on voit que pour passer de -1 à 255, il faut un tour complet (c'est à dire $-1$ + un tour = $-1 + 256 = 255$ ), il faut donc ajouter 256 = 2⁸ à -1 pour obtenir l'entier donnant son code.

De même, si l'on fait un tour complet dans le sens positif à partir de -6, on tombe sur 250 (c'est à dire $-6 + 256 = 250$ ). C'est donc l'écriture binaire de 250 qui donne le code complément à 2 sur 8 bits de -6.

Exercice 1☘

Donner le code de l'entier -100_dix avec la représentation "complément à deux sur 8 bits".

Réponse

-100 + 2⁸ = 156.

156 = 2⁷ + 2⁴ + 2³ + 2², d'où 156 = 1001 1100_deux.

En complément à deux sur 8 bits, -100 est codé 1001 1100.

Important

Ainsi un même code peut représenter 156 et -100... Il faut donc évidemment savoir de quel code il s'agit.

Par exemple en langage C, la valeur d'une variable de type signed short (entier signé sur 2 octets) sera codée en complément à deux sur 16 bits, tandis que la valeur d'une variable de type unsigned short (entier positif sur 2 octets) sera codé par son écriture usuelle en base deux.
C'est le type de la variable (donné par le programmeur en langage C) qui permet de savoir si le code doit être lu comme un code "complément deux" ou comme un code "écriture binaire usuelle".

Exercice 2☘

Donner le code en complément à deux sur un octet des entiers:

a = -126
b = +126
c = -1
d = 1

126 et 1

Le code des positifs est facile: il s'agit de l'écriture binaire usuelle.

b = 126 est donc codé par 0111 1110 en complément à deux sur 8 bits. c = 1 est codé par 0000 0001.

-126 et -1

Pour obtenir le code de -1, on ajoute 2⁸ = 256 à cette valeur. On obtient 255.
On calcule alors l' écriture binaire usuelle de 255: 255 = 1111 1111.
Le code en complément à deux sur un octet de l'entier -1 est donc 1111 1111.
Pour obtenir le code de -126, on ajoute 2⁸ = 256 à cette valeur. On obtient 130.
On calcule l'écriture binaire usuelle de 130:
130 = 2⁷ + 2¹ = 1000 0010_deux.
Le code en complément à deux sur un octet de l'entier -126 est donc 1000 0010.

Exercice 3☘

Le code suivant est le code binaire usuel d'un entier naturel: 1011 0101. Lequel?
Le code suivant est le code en complément à 2 sur 8 bits d'un entier: 1011 0101. Lequel?

code binaire

L'entier positif codé en binaire par 1011 0101 est l'entier 1011 0101_deux! Son code correspond à son écriture usuelle en base deux, il n'y a rien à calculer.

Toutefois, on est plus habitué à la base dix. En base dix, cet entier est $2^7+2^5+2^4+ 2^2+2^0 = 181$ .

code complément à 2

L'entier ainsi codé en complément à 2 est un négatif (puisque le bit de gauche est 1). Cet entier est 181 - $2^8$ = -75.