Codage en complément à deux sur n bits

Code en complément à 2 sur 4 bits.

Imaginer de même comment représenter sur un cercle un codage en complément à 2 sur 4 bits. Et donner le code de -1 puis celui de -6.

Une réponse

Dans ce cas, on ne partage plus le cercle en 2⁸ = 256 arcs égaux comme avec 8 bits, mais en 2⁴ = 16 arcs égaux.
Le cercle avec un code en complément à deux sur 4 bits:

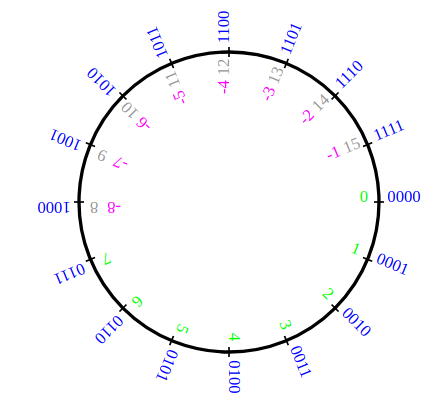
On voit que le code en complément à 2 sur 4 bits de -1 est donné par l'écriture binaire de 15 soit 1111. Le code de -6 serait donné par l'écriture binaire de 10 (-6 + un tour = -6 + 16 = 10), soit 1010.

Remarque

Un complément à deux sur 4 bits peut se définir ainsi:

• Un entier positif (entre 0 et $2^{3}-1 = 7$) est codé par son écriture binaire usuelle.
• Un entier négatif $n$ (entre $-2^3=-8$ et $-1$) est codé par l'écriture binaire du complément à $2^4$ de sa valeur absolue, c'est à dire par l'écriture binaire usuelle de l'entier positif $16 + n$.

Remarque

Dans la pratique, on n'utilise pas un tel code, car on code sur un nombre entier d'octets. On trouve en fait dans la pratique des codes sur 8 bits, 16 bits, 32 bits, 64 bits.

Code sur deux octets.

De la même façon, le code en complément à deux sur 2 octets (soit 16 bits) s'obtient comme suit:

• Un entier positif n compris entre 0 et 2¹⁵-1 = 32767 est codé sur 16 bits par son écriture binaire usuelle (le code commence donc à gauche par un 0).
• Un entier négatif n compris entre -2¹⁵ et -1 est codé par l'écriture binaire sur 16 bits de l'entier positif n + 2¹⁶ (soit n + un tour sur le cercle, le cercle étant cette fois découpé en 2¹⁶ arcs égaux).

Note

C'est par exemple ainsi que sont codés les signed short en langage C.

Important

Un complément à 2 sur 8 bits fait intervenir un complément à $2^8$,
un complément à 2 sur 16 bits fait intervenir un complément à $2^{16}$,
un complément à 2 sur $n$ bits fait intervenir un complément à $2^{n}$.

Exercice 5

Donner le code en complément à deux sur 16 bits des entiers suivants:

• a = 2
• b = -2
• c = 32767
• d = 32768
• e = -32767
• f = -32768

a

2_dix = 10_deux d'où le code: 0000 0000 0000 0010.

b

-2 + 2¹⁶ = 65534. 65534_dix = 1111 1111 1111 1110_deux.

Le code de -2 en complément à deux sur 16 bits est donc 1111 1111 1111 1110.

c

32767_dix = 111 1111 1111 1111_deux d'où le code en complément à deux sur 16 bits: 0111 1111 1111 1111.

d

C'est impossible! Les entiers codés en complément à deux sur 16 bits sont les entiers entre -32768 et +32767.

e

-32767 + 2¹⁶ = 32 769.

32 769_dix = 1000 0000 0000 0001_deux. Le code en complément à deux sur 16 bits de -32767 est donc 1000 0000 0000 0001.

f

-32768 + 2¹⁶ = 32 768.

32 768_dix = 1000 0000 0000 0000_deux. Le code en complément à deux sur 16 bits de -32768 est donc 1000 0000 0000 0000.