La fonction blog

On définit deux fonctions sur les entiers > 0.

Note

Ceux qui suivront la spécialité mathématiques en terminale découvriront la fonction "plus générale" logarithme.

La fonction dlog

Définition

Tout entier naturel $n$ (non nul) est compris entre deux puissances de 10: $10^k \leqslant n < 10^{k+1}$.

Le nombre $k$ sera appelé dlog(n).

Remarque: dlog(n) est donc le plus grand des entiers i vérifiant 10ⁱ ≤ n.

Exercice 1

Donner les valeurs de dlog(99), dlog(100), dlog(1000), dlog(101), dlog(1).

Solution

• $10 \leqslant 99 < 10^2$ donc dlog(99) = 1.
• $10^2 \leqslant 100 < 10^3$ donc dlog(100) = 2.
• $10^2 \leqslant 101 < 10^3$ donc dlog(101) = 2.
• $10^3 \leqslant 1000 < 10^4$ donc dlog(100) = 3.
• $10^0 \leqslant 1 < 10^1$ donc dlog(100) = 0.

Important

On retiendra:

Le nombre de chiffres dans l'écriture en base 10 d'un entier naturel $n$ (non nul) est égal à dlog(n)+1.

Exercice 2

Proposer un corps possible pour la fonction python suivante:

def dlog(n):
    """
    n -- entier naturel non nul
    renvoie dlog(n)
    """

Un code possible

def dlog(n):
    """
    n -- entier naturel non nul
    renvoie dlog(n)
    """
    k = 0
    p = 1 # contiendra les puissances de 10 successives
    while p <= n:
        k += 1
        p *= 10
    return k-1

La fonction blog

On définit la fonction blog de façon analogue à la fonction dlog mais en utilisant les puissances de 2.

Définition

Tout entier naturel $n$ (non nul) est compris entre deux puissances de 2: $2^k \leqslant n < 2^{k+1}$.

Le nombre $k$ sera appelé blog(n).

Remarque: blog(n) est donc le plus grand des entiers i vérifiant 2ⁱ ≤ n.

On aura le même lien avec l'écriture binaire d'un entier (écriture en base 2):

Propriété

Le nombre de chiffres dans l'écriture en base 2 d'un entier naturel $n$ (non nul) est égal à blog(n)+1.

En python, la fonction précédente dans laquelle 10 est remplacé par 2 donnera le résultat de blog(n):

def blog(n):
    """
    n -- entier naturel non nul
    renvoie blog(n)
    """
    k = 0
    p = 1 # contiendra les puissances de 2 successives
    while p <= n:
        k += 1
        p *= 2
    return k-1

Exercice 3

Donner les valeurs de blog(1), blog(2), blog(3), blog(4).

Solution

• $2^0 \leqslant 1 < 2^1$: blog(1) = 0.
• $2^1 \leqslant 2 < 2^2$: blog(2) = 1.
• $2^1 \leqslant 3 < 2^2$: blog(3) = 1.
• $2^2 \leqslant 4 < 2^3$: blog(1) = 2.

Exercice 4

On construit un arbre comme ci-dessous.

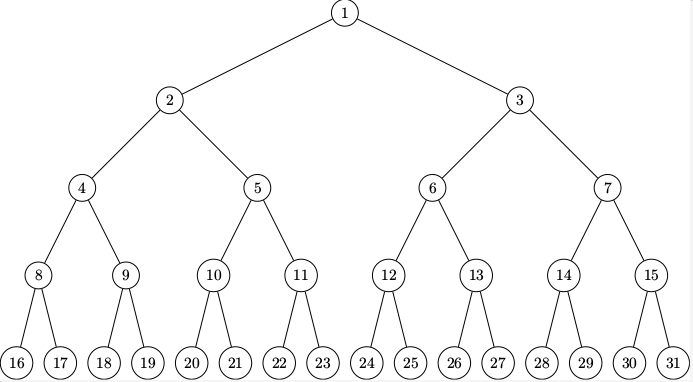
On a arrêté la construction... mais il est évident que l'on peut la poursuivre ainsi autant qu'on veut.

Comment utiliser cet arbre pour calculer blog(n) où n est un entier ?

Remarque

Pour dessiner cet arbre, vous remarquerez que:

• Chaque sommet a exactement deux fils (un fils gauche et un fils droit). Les fils des sommets du niveau le plus bas dessiné ne sont pas représentés mais vous pouvez aisément les imaginer.
• les sommets sont numérotés de haut en bas et de droite à gauche dans l'ordre usuel.

Vous remarquerez également que cette façon de numéroter donne une formule simple:

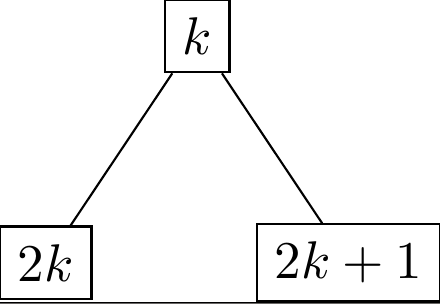
• le fils gauche du sommet marqué k est marqué 2k,
• le fils droit du sommet marqué k est marqué 2k+1.

Lien avec blog

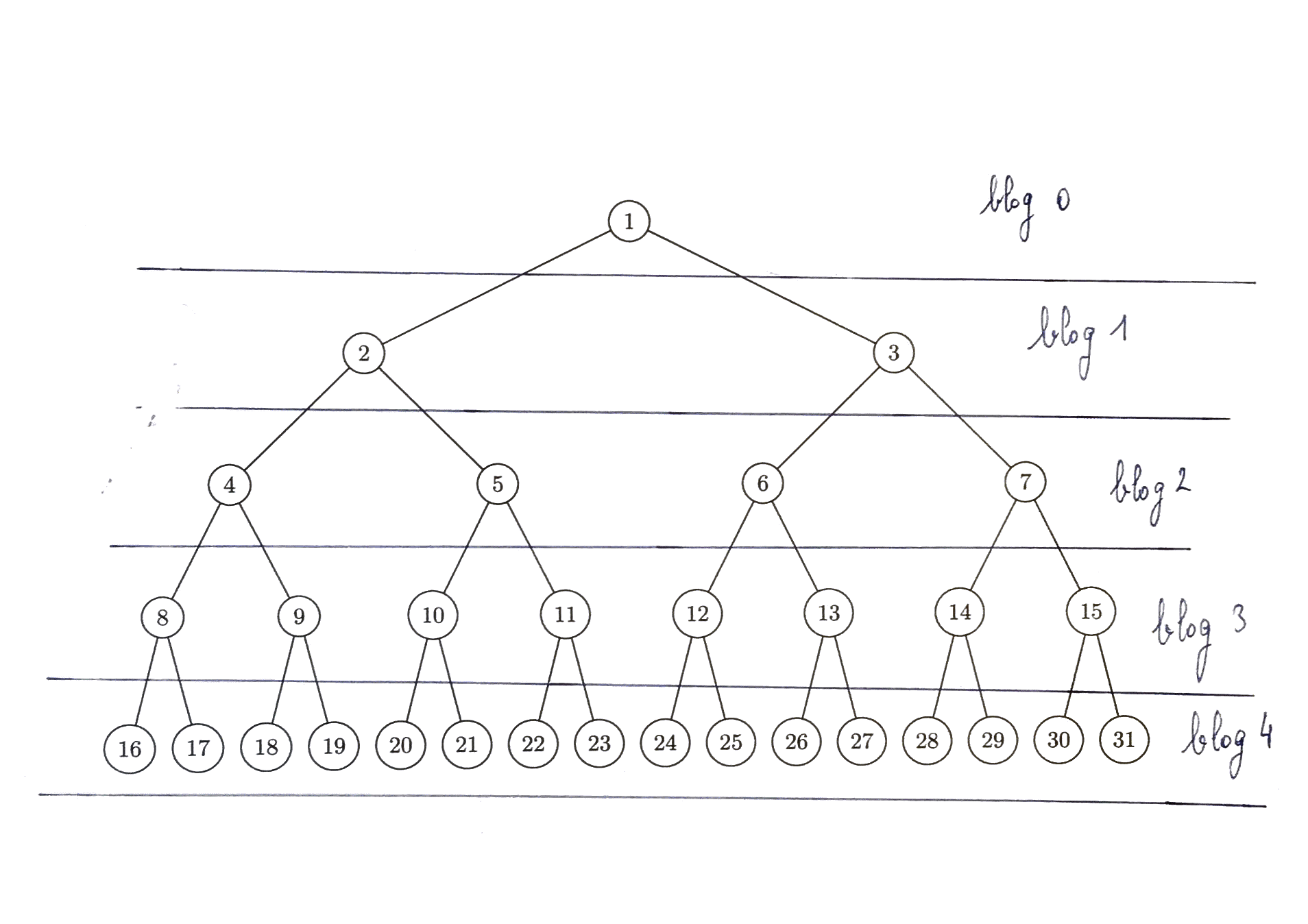
blog(n) correspond tout simplement au niveau de profondeur dans l'arbre, comme illustré sur la figure ci-dessous.

Exercice 5

Plus k est grand, plus le nombre d'entiers n tels que blog(n) = k est grand (cela se visualise bien avec l'arbre de l'exercice précédent).

Pourriez-vous dire plus précisément combien d'entiers n vérifie blog(n) = k ?

Solution

On peut déjà répondre pour les premiers entiers en observant l'arbre de l'exercice précédent:

• 1 entier vérifie blog(n) = 0.
• 2 entiers vérifient blog(n) = 1.
• 4 entiers vérifient blog(n) = 2.
• 8 entiers vérifient blog(n) = 3.
• 16 entiers vérifient blog(n) = 4.

On conjecture, avec ce qui précède, qu'il y a 2^k entiers n tels que blog(n) = k.

Preuve.

Les entiers n tels que blog(n) = k sont les entiers n tels que $2^k \leqslant n < 2^{k+1}$.
Il y en a $C = 2^{k+1} - 2^k$.
En factorisant $2^k$ dans cette expression: $C = 2^k \times \left( 2 - 1\right)$.
On a donc bien $\boxed{C = 2^k}$.