Exercices: déterminer une racine lorsqu'on en connaît déjà une

Exercice

Soit $f\colon x\longmapsto 4x^2-8x-12$ un trinôme.

Vérifier que $-1$ est racine de $f$ puis déterminer les racines de $f$.

Résolution, rédaction 1

On calcule $f(-1)$:

$$\begin{align*} f(-1) &= 4(-1)^2-8(-1)-12\\ &= 4 +8-12\\ &= 0\\ \end{align*}$$

$-1$ est donc racine de $f$ et le nombre $s$ tel que $\frac{-1+s}{2} = \frac{-b}{2a}$, c'est à dire $s = -\frac{b}{a}+1 = 3$ est la seconde racine.

Résolution, rédaction 2

On vérifie par le calcul que l'on a bien $f(-1)=0$.

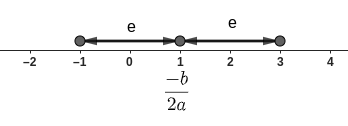
On détermine l'écart e entre $\frac{-b}{2a} = 1$ et la racine $r=-1$: $e = 2$. On reporte cet écart de "l'autre côté": $\frac{-b}{2a} +e =3$: la seconde racine est 3.

Exercice

Soit $f\colon x\longmapsto -3x^2-30x-75$ un trinôme.

Vérifier que $-5$ est racine de $f$ puis déterminer les racines de $f$.

Résolution, rédaction 1

On calcule $f(-5)$:

$$\begin{align*} f(-5) &= -3(-5)^2-30(-5)-75\\ &= -75+150-75\\ &= 0\\ \end{align*}$$

$r=-5$ est donc racine de $f$. Le nombre $s$ tel que $\frac{-5+s}{2} = \frac{-b}{2a}$, c'est à dire $s = -\frac{b}{a}+5$ a pour valeur $-5$.

Il n'y a donc qu'une seule racine: $-5$.

Résolution, rédaction 2

L'écart e entre $\frac{-b}{2a} = -5$ et la racine $r=-5$ est égal à 0. Il n'y a donc qu'une seule racine.