Des formules

Discriminant

Soit $f\colon x\longmapsto ax^2+bx+c$ une équation du second degré. On appelle discriminant de cette équation le nombre $\Delta = b^2-4ac$.

Théorème

L'équation $ax^2+bx+c=0$, d'inconnue $x\in\mathbb{R}$, possède 0 ou 1 ou 2 solutions. Plus précisément:

• si $\Delta <0$, l'équation n'a pas de solution dans $\mathbb{R}$.
• si $\Delta =0$, l'équation a une unique solution dans $\mathbb{R}$: le nombre $\frac{-b}{2a}$.
• si $\Delta >0$, l'équation a deux solutions dans $\mathbb{R}$: les nombres $\frac{-b}{2a} + \frac{\sqrt{\Delta}}{2a}$ et $\frac{-b}{2a} - \frac{\sqrt{\Delta}}{2a}$.

preuve

Les deux racines sont symétriques par rapport à l'abscisse du sommet.

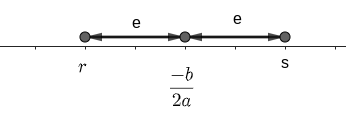
On peut les chercher sous la forme $\frac{-b}{2a}+e$ et $\frac{-b}{2a}-e$ mettant en évidence cette symétrie.

On cherche $x$ racine de $f$ avec $x=\frac{-b}{2a}+e$, c'est à dire $e = x-\frac{-b}{2a}$ (écart entre $x$ et l'abscisse $\frac{-b}{2a}$ du sommet).

On a:

$$\begin{align*} f(x) &= f\left(\frac{-b}{2a}+e\right)\\ &= a\left(e+\frac{-b}{2a}\right)^2+b\left(e+\frac{-b}{2a}\right)+c\\ &= a\left(e^2+\frac{-be}{a} + \frac{b^2}{4a^2} \right) +be+\frac{-b^2}{2a}+c\\ &= ae^2-be + \frac{b^2}{4a} +be+\frac{-b^2}{2a}+c\\ &= ae^2 + \frac{b^2}{4a} +\frac{-b^2}{2a}+c\\ &= ae^2 + \frac{b^2}{4a} +\frac{-2b^2}{4a}+c\\ &= ae^2 - \frac{b^2}{4a} +c\\ &= ae^2 - \frac{b^2}{4a} +\frac{4ac}{4a}\\ &= ae^2 - \frac{\Delta}{4a} \end{align*}$$

On a donc:

$$\begin{align*} f(x) = 0 &\Longleftrightarrow ae^2 - \frac{\Delta}{4a} = 0 \\ &\Longleftrightarrow ae^2 = \frac{\Delta}{4a} \\ &\Longleftrightarrow e^2 = \frac{\Delta}{4a^2} \\ &\Longleftrightarrow \left(x-\frac{-b}{2a}\right)^2 = \frac{\Delta}{4a^2} \\ \end{align*}$$

Cas du discriminant strictement négatif.

$f(x) = 0 \Longleftrightarrow \left(x-\frac{-b}{2a}\right)^2 = \frac{\Delta}{4a^2}$

Le carré d'un réel est un nombre de l'intervalle $\left[0~;~+\infty\right[$: il n'existe donc aucun réel $x$ tel que $\left(x-\frac{-b}{2a}\right)^2 = \Delta$ avec $\Delta\in \left]-\infty~;~0\right[$. L'équation $ax^2+bx+c=0$ est donc sans solution dans $\mathbb{R}$.

Cas du discriminant nul.

On a $f(x) = 0 \Longleftrightarrow \left(x-\frac{-b}{2a}\right)^2 = \frac{\Delta}{4a^2}$, soit
$f(x) = 0 \Longleftrightarrow \left(x-\frac{-b}{2a}\right)^2 = 0$ ou encore $ax^2+bx+c=0\Longleftrightarrow x-\frac{-b}{2a} = 0$.

L'équation a donc une unique solution dans $\mathbb{R}$: le nombre $\frac{-b}{2a}$.

Cas du discriminant strictement positif

On a $f(x) = 0 \Longleftrightarrow \left(x-\frac{-b}{2a}\right)^2 = \frac{\Delta}{4a^2}$, soit

$ax^2+bx+c=0\Longleftrightarrow x-\frac{-b}{2a} = \frac{-\sqrt{\Delta}}{2a} \text{ ou } x-\frac{-b}{2a} = \frac{+\sqrt{\Delta}}{2a}$.

L'équation a donc deux solutions dans $\mathbb{R}$: les nombres $\frac{-b}{2a} + \frac{\sqrt{\Delta}}{2a}$ et $\frac{-b}{2a} - \frac{\sqrt{\Delta}}{2a}$.

Remarque

Dans la preuve ci-dessus, on a obtenu $f(x) = ae^2 - \frac{\Delta}{4a}$ soit $ax^2+bx+c = a\left(x+\frac{b}{2a}\right)^2 - \frac{\Delta}{4a}$. Cette écriture de $f$ est ce que l'on nomme forme canonique de $f$. On pourrait la nommer de façon plus appropriée forme symétrique de f ou encore forme sommet de $f$ puisqu'elle met en évidence l'axe de symétrie (d'équation $x=\frac{-b}{2a}$) de la parabole et les coordonnées du sommet de cette parabole $\Omega\left(\frac{-b}{2a}~;~-\frac{\Delta}{4a}\right)$.