La fonction blog

Attention

Cette page n'est pour le moment pas une priorité. Travaillez là uniquement si vous en avez le temps, c'est à dire si le reste est travaillé et su. Nous reviendrons dessus plus tard dans l'année lorsque nous en aurons besoin.

On définit la fonction blog de façon analogue à la fonction dlog mais en utilisant les puissances de 2.

Définition

Tout entier naturel $n$ (non nul) est compris entre deux puissances de 2: $2^k \leqslant n < 2^{k+1}$.

Le nombre $k$ sera appelé blog(n).

On aura le même lien avec l'écriture binaire d'un entier (écriture en base 2):

Propriété

Le nombre de chiffres dans l'écriture en base 2 d'un entier naturel $n$ (non nul) est égal à blog(n)+1.

En python, un calcul de blog(n):

def blog(n):
    """
    n -- entier naturel non nul
    renvoie blog(n)
    """
    k = 0
    p = 1 # contiendra les puissances de 2 successives
    while p <= n:
        k += 1
        p *= 2
    return k-1

Exercice 1

Donner les valeurs de blog(1), blog(2), blog(3), blog(4).

Solution

• $2^0 \leqslant 1 < 2^1$: blog(1) = 0.
• $2^1 \leqslant 2 < 2^2$: blog(2) = 1.
• $2^1 \leqslant 3 < 2^2$: blog(3) = 1.
• $2^2 \leqslant 4 < 2^3$: blog(1) = 2.

Exercice 2

On construit un arbre comme ci-dessous.

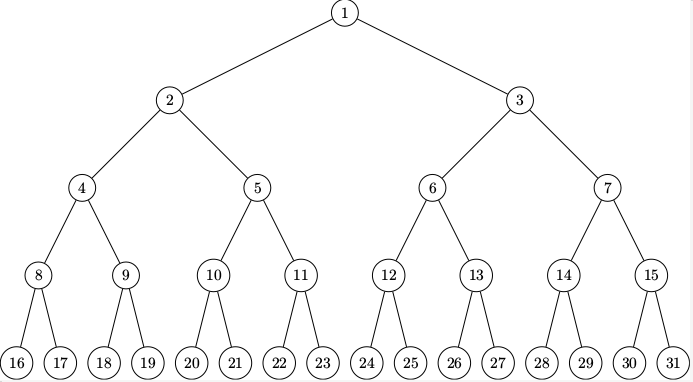
On a arrêté la construction... mais il est évident que l'on peut la poursuivre ainsi autant qu'on veut.

Comment utiliser cet arbre pour déterminer l'écriture binaire d'un entier n > 0 ?

Remarque

Pour dessiner cet arbre, vous remarquerez que:

• Chaque sommet a exactement deux fils (un fils gauche et un fils droit). Les fils des sommets du niveau le plus bas dessiné ne sont pas représentés mais vous pouvez aisément les imaginer.
• les sommets sont numérotés de haut en bas et de droite à gauche dans l'ordre usuel.

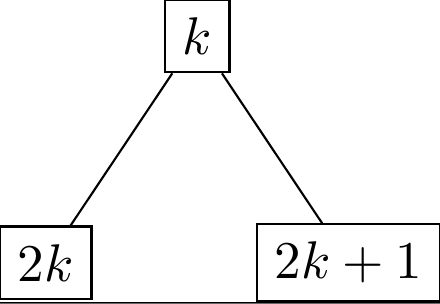
Vous remarquerez également que cette façon de numéroter donne une formule simple:

• le fils gauche du sommet marqué k est marqué 2k,
• le fils droit du sommet marqué k est marqué 2k+1.

Ecriture binaire

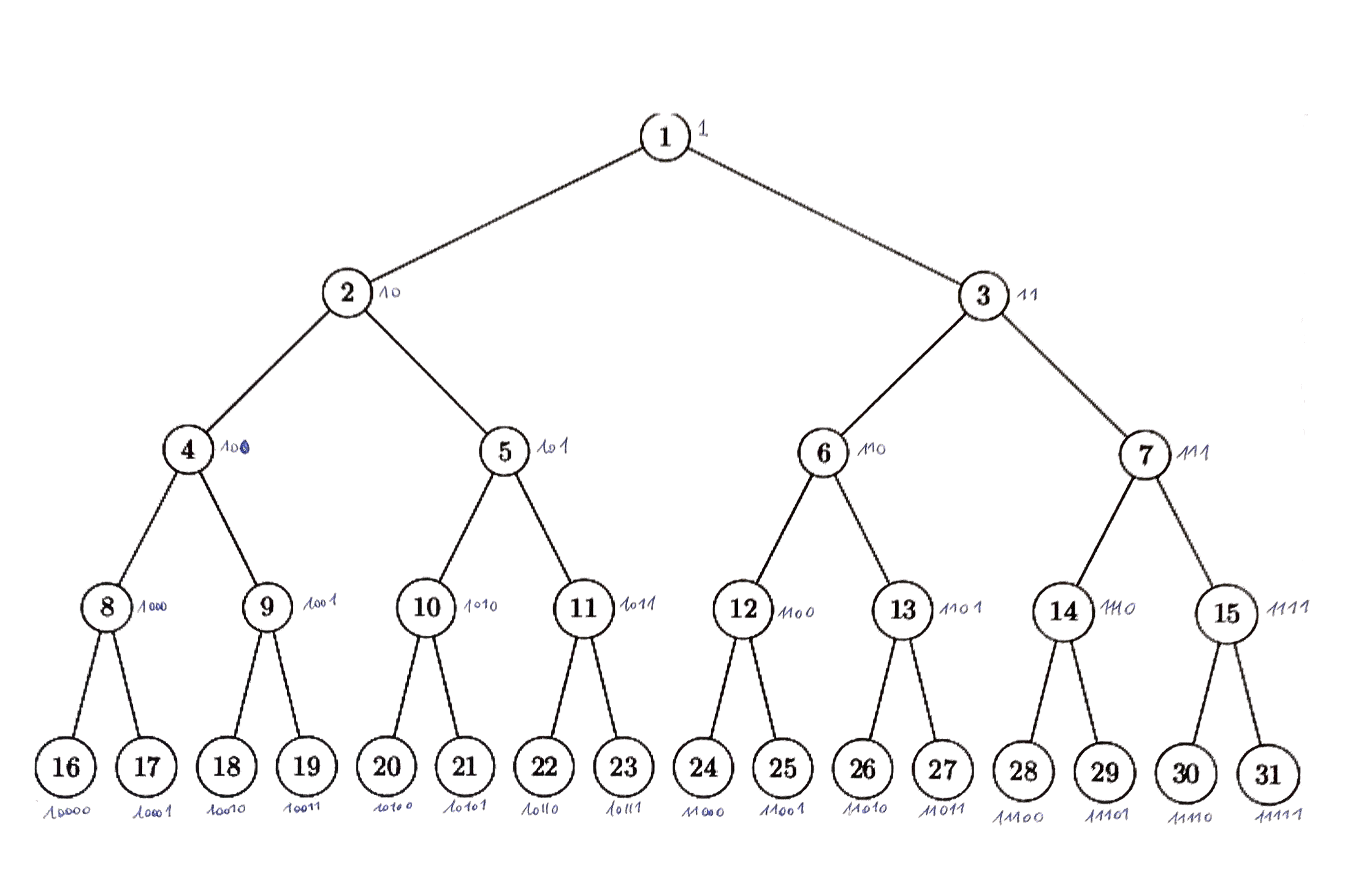
A partir de l'écriture d'un entier k:

• on obtient l'écriture de son fils gauche (c'est à dire 2k) en ajoutant un 0 en fin d'écriture,
• et on obtient l'écriture de son fils droit (c'est à dire 2k+1) en ajoutant un 1 en fin d'écriture.

En partant de la racine (écriture 1), on peut donc en déduire très mécaniquement l'écriture de tous les entiers.

Remarque

Vous remarquerez que tous les nombres d'un même niveau dans l'arbre ont une écriture binaire utilisant le même nombre de chiffres.

Avec le lien "nombre de bits = blog(n)+1", ceci est une autre façon d'écrire que tous les entiers se trouvant à un même niveau dans l'arbre ont le même blog.