Du décimal vers le binaire

Les divisions en cascade

Rappelons comment on peut obtenir les chiffres, un à un, d'une écriture décimale.

Raisonnons sur l'exemple de l'entier $n = 8643$.

• Le chiffre des unités de $n$ est le reste de la division euclidienne de $n$ par $10$:
  
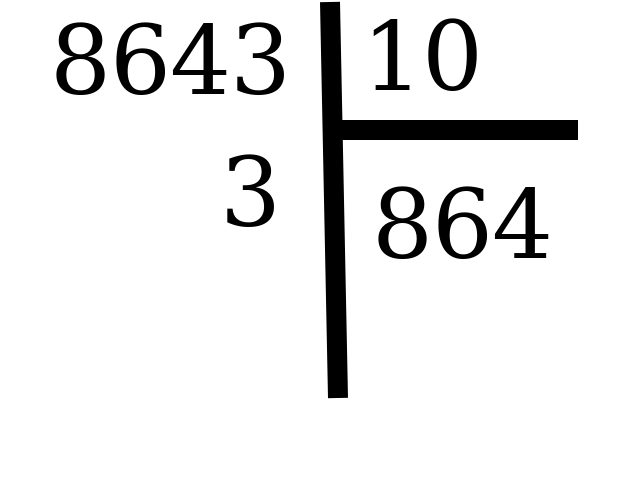
  Le chiffre des unités est donc 3.

• Le chiffre des dizaines est le chiffre des unités du quotient précédent:
  
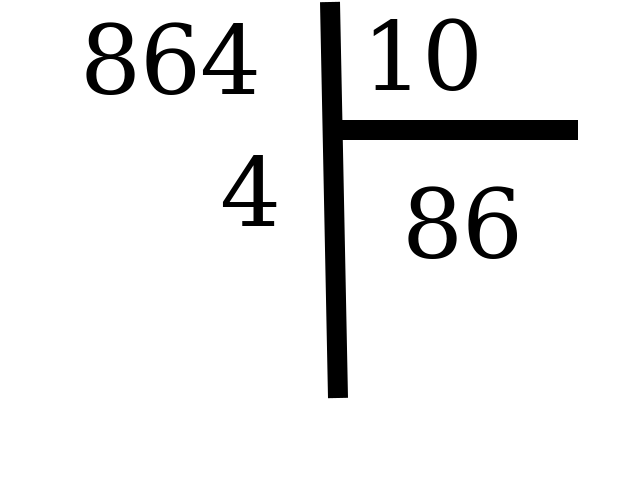
  Le chiffre des dizaines est donc 4.

• Et on continue ainsi jusqu'à obtenir un quotient nul.

On peut résumer ceci par une "division en cascade":

Dans cette division en cascade, on voit que les restes successifs (chiffres rouges) sont les chiffres de l'entier (obtenu à contre-sens de l'écriture usuelle puisqu'on obtient en premier le chiffre des unités).

Lorsqu'on obtient un quotient (nombres noirs) nul, on arrête la cascade.

La division en cascade en base 2.

En remplaçant le diviseur 10 par le diviseur 2 dans une division en cascade, on obtiendra les chiffres de l'écriture binaire de l'entier.

La cascade suivante permet par exemple de constater que 13_dix = 1101_deux.

Exercice.

Obtenir l'écriture binaire des entiers suivants par des divisions en cascade.

1. $n = 34$
2. $m = 17$.

Solution

1. On pose notre division en cascade:
   
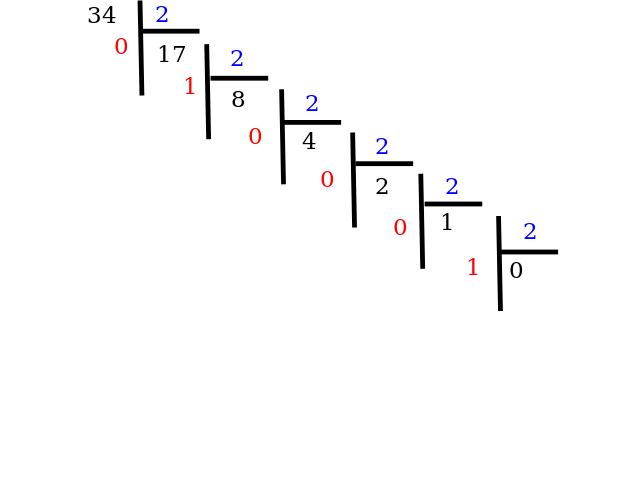
   L'écriture binaire est donc $34 = 100010_{\text{deux}}$.
   On peut "vérifier": $2^1+ 2^5 = 2+32=34$.

2. On pose notre division en cascade:
   
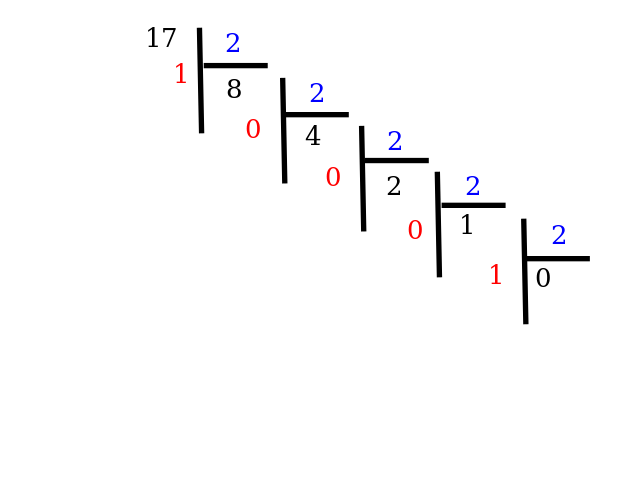
   L'écriture binaire est donc $17 = 10001_{\text{deux}}$.
   On peut "vérifier": $2^0+ 2^4 = 1+16=17$.