Un exercice de sujet de baccalauréat☘
Les exercices dans les sujets NSI de terminale peuvent porter sur des thèmes du programme de première.
C'est le cas de l'exercice 4 de ce sujet de 2021 dont vous trouverez l'énoncé ci-dessous et que vous chercherez à résoudre.
Partie A: représentation d'un labyrinthe.☘
On modélise un labyrinthe par un tableau à deux dimensions:
- n lignes
- m colonnes
où n et m sont des entiers strictement positifs.
- Les lignes sont numérotées de 0 à n-1.
- Les colonnes sont numérotées de 0 à m-1.
- La case en haut à gauche est repérée par (0,0).
- La case en bas à droite par (n-1, m-1).
Dans ce tableau:
- 0 représente une case vide (hors case de départ et case d'arrivée).
- 1 représente un mur.
- 2 représente le départ (l'entrée) du labyrinthe.
- 3 représente l'arrivée (la sortie) du labyrinthe.
Exemple
Ainsi, en Python, le labyrinthe ci-dessous (où D marque la case d'entrée et A la case de sortie)
est représenté par la liste de listes lab1:

lab1 = [[1,1,1,1,1,0,0,0,0,0,1],
[1,0,0,0,1,0,1,0,1,0,1],
[1,0,1,0,1,0,1,0,1,0,1],
[1,0,1,0,1,0,1,0,1,0,1],
[1,0,1,0,1,0,1,0,1,0,1],
[2,0,1,0,0,0,1,0,1,0,3],
[1,1,1,1,1,1,1,0,1,0,1],
[1,0,0,0,1,0,0,0,1,0,1],
[1,0,1,0,1,0,1,1,1,0,1],
[1,0,1,1,1,0,1,0,0,0,1],
[1,0,0,0,0,0,1,1,0,1,1]]
Question☘
Le tableau de tableaux dont le code python est donné ci-dessous:
lab2 = [ [1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,0,1],
[1,0,1,0,0,0,1],
[1,0,1,0,1,0,1],
[1,0,0,0,1,0,1],
[1,1,1,1,1,3,1]]
est censé représenter le labyrinthe suivant:
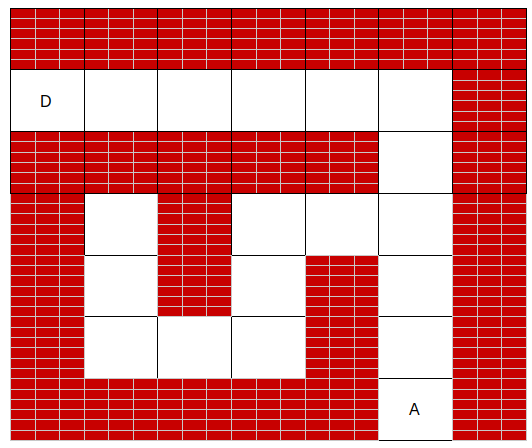
Mais un mur se trouve dans la cellule du tableau qui devrait contenir la case de départ.
Donner une instruction permettant de modifier lab2 en plaçant la case départ au bon endroit.
Solution
lab2[1][0] = 2
Question☘
Écrire une fonction est_valide(i, j, n, m) qui renvoie True lorsque le couple (i, j) correspond
à des coordonnées valides pour un labyrinthe de taille (n,m) et qui renvoie False sinon.
Exemples d'appels:
>>> est_valide(5, 2, 10, 10)
True
>>> est_valide(-3, 4, 10, 10)
False
Solution
def est_valide(i, j, n, m):
return 0 <= i <= n-1 and 0 <= j <= m-1
Question☘
On suppose que le départ d'un labyrinthe est toujours indiqué, mais on ne fait aucune supposition sur son emplacement.
Compléter la fonction depart(lab) ci-dessous de sorte qu'elle renvoie, sous la forme d'un tuple, les coordonnées (ligne, colonne)
du départ d'un labyrinthe (représenté par le paramètre lab).
Exemple.
En utilisant lab1 défini en début d'énoncé:
>>> depart(lab1)
(5, 0)
Le code à compléter:
def depart(lab):
n = len(lab)
m = len(lab[0])
....
Solution
def depart(lab):
n = len(lab)
m = len(lab[0])
for ligne in range(0,n):
for colonne in range(0,m):
if lab[ligne][colonne] == 2:
return (ligne, colonne)
Question☘
Écrire une fonction nb_cases_vides(lab) qui renvoie le nombre de cases vides d'un labyrinthe (la case d'arrivée et la case
de départ sont comptées comme cases vides).
Exemple.
En utilisant la version corrigée de lab2:
>>> nb_cases_vides(lab2)
19
Solution
def nb_cases_vides(lab):
n = len(lab)
m = len(lab[0])
compteur = 0
for ligne in range(0,n):
for colonne in range(0,m):
if lab[ligne][colonne] in (0, 2, 3):
compteur += 1
return compteur
Partie B: recherche d'une solution dans un labyrinthe.☘
On suppose dans cette partie que chaque labyrinthe possède un unique chemin allant du départ à l'arrivée sans repasser par une même case. Dans la suite, ce chemin est nommé solution du labyrinthe.
Pour déterminer la solution d'un labyrinthe, on parcourt les cases vides de proche en proche. Lors d'un tel parcours, afin d'éviter de tourner en rond, on choisit de marquer les cases visitées. Pour cela, on remplace la valeur d'une case visitée dans le tableau représentant le labyrinthe par la valeur 4.
Question☘
On dit que deux cases d'un labyrinthe sont voisines lorsqu'elles ont un côté commun.
On suppose disposer d'une fonction voisines(i, j, lab) qui
- prend en argument deux entiers i et j représentant les coordonnées d'une case et un tableau lab qui représente un labyrinthe.
- renvoie la liste des coordonnées des cases voisines de la case (i, j) qui sont valides, non visitées et qui ne sont pas des murs (l'ordre des éléments de cette liste n'importe pas).
Exemple.
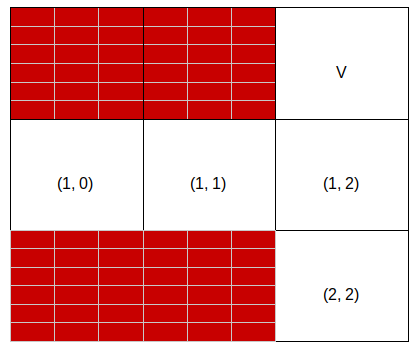
>>> voisines(1, 1, [ [1,1,1], [4,0,0], [1,0,1]])
[(2,1), (1,2)]
1) Que renvoie l'appel ci-dessous ?
>>> voisines(1, 2, [[1,1,4], [0,0,0],[1,1,0]])
Solution
On obtient:
[(1, 1), (2, 2)]
2) Proposer un code python pour la fonction voisines.
Solution
Un code possible:
def voisines(i, j, lab):
n = len(lab)
m = len(lab[0])
voisins = [(i,j-1), (i-1,j), (i+1,j), (i, j+1)]
voisins_valides = [x for x in voisins if est_valide(x[0], x[1], n, m)]
return [x for x in voisins_valides if lab[x[0]][x[1]] != 1 and lab[x[0]][x[1]] != 4]
Question☘
On souhaite stocker la solution d'un labyrinthe dans une liste chemin.
Cette liste contiendra les coordonnées des cases de la solution, dans l'ordre.
Pour cela, on procède de la façon suivante:
- Initialement:
- déterminer les coordonnées du départ: c'est la première case à visiter.
- ajouter les coordonnées de la case départ à la liste
chemin.
- Tant que l'arrivée n'est pas atteinte:
- on marque la case visitée avec la valeur 4.
- si la case visitée possède une case voisine libre: la première case de la liste renvoyée par la fonction
voisinesdevient la prochaine case à visiter et on ajoute cette case voisine à la listechemin. - sinon: il s'agit d'une impasse. Dans ce cas, on supprime la dernière case de la liste
chemin. La prochaine case à visiter est celle qui est désormais en dernière position de la listechemin.
Application à un cas particulier☘
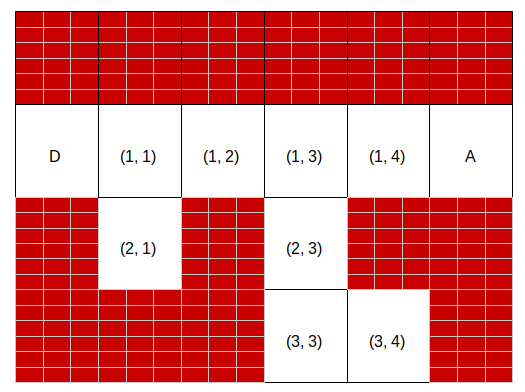
Le tableau de tableaux lab3 ci-dessous représente un labyrinthe:
lab3 = [[1,1,1,1,1,1],
[2,0,0,0,0,3],
[1,0,1,0,1,1],
[1,1,1,0,0,1]]
La suite d'instructions ci-dessous simule le début des modifications subies par la liste chemin lorsqu'on applique la méthode
présentée ci-dessus.
# entrée (1,0), sortie (1,5)
chemin = [(1,0)]
chemin.append((1,1))
chemin.append((2,1))
chemin.pop()
chemin.append((1,2))
chemin.append((1,3))
chemin.append((2,3))
Compléter cette suite d'instructions jusqu'à ce que la liste chemin représente la solution du labyrinthe lab3.
Rappel
La méthode pop supprime le dernier d'une liste (et renvoie cet élément).
Solution
# entrée (1,0), sortie (1,5)
chemin = [(1,0)]
chemin.append((1,1)) # chemin = [(1,0), (1,1)]
chemin.append((2,1)) # chemin = [(1,0), (1,1), (2,1)]
chemin.pop() # chemin = [(1,0), (1,1)]
chemin.append((1,2)) # chemin = [(1,0), (1,1), (1,2)]
chemin.append((1,3)) # chemin = [(1,0), (1,1), (1,2), (1,3)]
chemin.append((2,3)) # chemin = [(1,0), (1,1), (1,2), (1,3), (2,3)]
chemin.append((3,3)) # chemin = [(1,0), (1,1), (1,2), (1,3), (2,3), (3,3)]
chemin.append((3,4)) # chemin = [(1,0), (1,1), (1,2), (1,3), (2,3), (3,3), (3,4)]
chemin.pop() # chemin = [(1,0), (1,1), (1,2), (1,3), (2,3), (3,3)]
chemin.pop() # chemin = [(1,0), (1,1), (1,2), (1,3), (2,3)]
chemin.pop() # chemin = [(1,0), (1,1), (1,2), (1,3)]
chemin.append((1,4)) # chemin = [(1,0), (1,1), (1,2), (1,4)]
chemin.append((1,5)) # chemin = [(1,0), (1,1), (1,2), (1,4), (1,5)]
Remarque
Le déroulé précédent dépend bien entendu de l'ordre dans lequel on parcourt les voisins d'une cellule.
Dans le cas de lab3, si le voisin droit d'une cellule (c'est à dire le voisin (i, j+1) de (i, j)) était toujours
listé en premier, la recherche du chemin solution se ferait ici sans aucun pop.
Traitement du cas général☘
Compléter la fonction solution(lab) commencée ci-dessous de sorte qu'elle renvoie le chemin solution du labyritnhe représenté
par le paramètre lab.
Indication
Penser à utiliser la fonction voisines.
def solution(lab):
chemin = [depart(lab)]
case = chemin[0]
i, j = case[0], case[1]
....
Exemple:
>>> solution(lab2)
[(1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (1, 5),
(2, 5), (3, 5), (4, 5), (5, 5), (6, 5)]
Solution
def solution(lab):
case = depart(lab)
chemin = [case]
i, j = case[0], case[1]
while lab[i][j] != 3:
lab[i][j] = 4
voisinage = voisines(i, j, lab)
if voisinage != [] :
chemin.append(voisinage[0])
else:
chemin.pop()
# mise à jour de la prochaine case à visiter:
case = chemin[-1]
i, j = case[0], case[1]
return chemin
Le code complet☘
On donne ci-dessous un récapitulatif des codes utilisés dans les questions de l'exercice.
On a ajouté une fonction de dessin des labyrinthes basé sur le module turtle.
Exemple d'appel.
L'appel affichage(lab2, soluce = True) donne
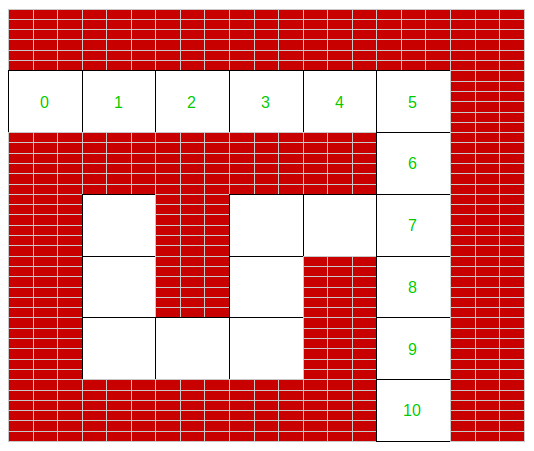
Le code
#######################################
### Définition des labyrinthes
#######################################
lab1 = [ [1,1,1,1,1,0,0,0,0,0,1],
[1,0,0,0,1,0,1,0,1,0,1],
[1,0,1,0,1,0,1,0,1,0,1],
[1,0,1,0,1,0,1,0,1,0,1],
[1,0,1,0,1,0,1,0,1,0,1],
[2,0,1,0,0,0,1,0,1,0,3],
[1,1,1,1,1,1,1,0,1,0,1],
[1,0,0,0,1,0,0,0,1,0,1],
[1,0,1,0,1,0,1,1,1,0,1],
[1,0,1,1,1,0,1,0,0,0,1],
[1,0,0,0,0,0,1,1,0,1,1]]
lab2 = [ [1,1,1,1,1,1,1],
[2,0,0,0,0,0,1],
[1,1,1,1,1,0,1],
[1,0,1,0,0,0,1],
[1,0,1,0,1,0,1],
[1,0,0,0,1,0,1],
[1,1,1,1,1,3,1]]
BQ1_2 = [[1,1,4], [0,0,0],[1,1,0]]
lab3 = [[1,1,1,1,1,1],
[2,0,0,0,0,3],
[1,0,1,0,1,1],
[1,1,1,0,0,1]]
##########################################
#### les fonctions de l'exercice
##########################################
def est_valide(i, j, n, m):
return 0 <= i <= n-1 and 0 <= j <= m-1
def depart(lab):
n = len(lab)
m = len(lab[0])
for ligne in range(0,n):
for colonne in range(0,m):
if lab[ligne][colonne] == 2:
return (ligne, colonne)
def nb_cases_vides(lab):
n = len(lab)
m = len(lab[0])
compteur = 0
for ligne in range(0,n):
for colonne in range(0,m):
if lab[ligne][colonne] in (0, 2, 3):
compteur += 1
return compteur
def voisines(i, j, lab):
n = len(lab)
m = len(lab[0])
voisins = [(i,j-1), (i-1,j), (i+1,j), (i, j+1)]
voisins_valides = [x for x in voisins if est_valide(x[0], x[1], n, m)]
return [x for x in voisins_valides if lab[x[0]][x[1]] != 1 and lab[x[0]][x[1]] != 4]
def solution(lab):
case = depart(lab)
chemin = [case]
i, j = case[0], case[1]
while lab[i][j] != 3:
lab[i][j] = 4
voisinage = voisines(i, j, lab)
if voisinage != [] :
chemin.append(voisinage[0])
else:
chemin.pop()
# mise à jour de la prochaine case à visiter:
case = chemin[-1]
i, j = case[0], case[1]
return chemin
##########################################
### une fonction de représentation
### qui s'appuie sur le module turtle
##########################################
from turtle import *
def affichage(lab, soluce = False):
def rectangle(xbg, ybg, largeur, hauteur, r, g, b):
color((r, g, b))
penup()
goto(xbg,ybg)
pendown()
goto(xbg + largeur, ybg)
goto(xbg + largeur, ybg + hauteur)
goto(xbg, ybg + hauteur)
goto(xbg, ybg)
def rectangle_plein(xbg, ybg, largeur, hauteur, r, g, b):
color((200, 200, 200))
fillcolor((r, g, b))
penup()
goto(xbg,ybg)
pendown()
begin_fill()
goto( xbg + largeur, ybg )
goto( xbg + largeur, ybg + hauteur)
goto(xbg, ybg + hauteur)
goto(xbg,ybg)
end_fill()
def brique(xbg, ybg, largeur):
rectangle_plein(xbg, ybg, largeur, largeur//2, 200, 200, 200)
epsilon = largeur//20
rectangle_plein(xbg+epsilon, ybg+epsilon, largeur-2*epsilon, largeur//2-2*epsilon, 200, 0, 0)
def mur(xbg, ybg, largeur, hauteur):
largeur_brique = largeur//3
hauteur_brique = largeur_brique//2
for r in range(0, hauteur, hauteur_brique):
for k in range(0, largeur, largeur_brique):
brique(xbg + k, ybg + r, largeur_brique)
def dessine_dedale(tab):
nb_lignes = len(tab)
nb_colonnes = len(tab[0])
for ligne in range(0, nb_lignes):
for colonne in range(0, nb_colonnes):
rectangle(colonne*cote, (nb_lignes-1-ligne)*cote, cote, cote, 0, 0, 0)
if tab[ligne][colonne] == 1:
mur(colonne*cote, (nb_lignes-1-ligne)*cote, cote, cote)
elif tab[ligne][colonne] == 2:
penup()
goto(colonne*cote+cote/2, (nb_lignes-1-ligne)*cote+cote/3)
write("D", align="center", font=("Arial", 12, "normal"))
elif tab[ligne][colonne] == 3:
penup()
goto(colonne*cote+cote/2, (nb_lignes-1-ligne)*cote+cote/3)
write("A", align="center", font=("Arial", 12, "normal"))
elif tab[ligne][colonne] == 4:
penup()
goto(colonne*cote+cote/2, (nb_lignes-1-ligne)*cote+cote/3)
write("V", align="center", font=("Arial", 12, "normal"))
else:
penup()
goto(colonne*cote+cote/2, (nb_lignes-1-ligne)*cote+cote/3)
write(f"({ligne}, {colonne})", align="center", font=("Arial", 12, "normal"))
def dessine_solution(lab):
nb_lignes = len(lab)
nb_colonnes = len(lab[0])
for ligne in range(0, nb_lignes):
for colonne in range(0, nb_colonnes):
rectangle(colonne*cote, (nb_lignes-1-ligne)*cote, cote, cote, 0, 0, 0)
if lab[ligne][colonne] == 1:
mur(colonne*cote, (nb_lignes-1-ligne)*cote, cote, cote)
color((0, 200, 0))
for num, case in enumerate(solution(lab)):
penup()
goto(case[1]*cote+cote/2, (nb_lignes-1-case[0])*cote+cote/3)
write(f"{num}", align="center", font=("Arial", 12, "normal"))
nb_lignes = len(lab)
nb_colonnes = len(lab[0])
cote = 6
setworldcoordinates(-1*cote,-1*cote, (nb_colonnes+1)*cote, (nb_lignes+1)*cote)
colormode(255)
delay(0)
if soluce:
dessine_solution(lab)
else:
dessine_dedale(lab)
hideturtle()
mainloop()