Un exercice de sujet de baccalauréat☘

Les exercices dans les sujets NSI de terminale peuvent porter sur des thèmes du programme de première.

C'est le cas de l'exercice 2 de ce sujet de 2021 dont vous retrouverez l'énoncé ci-dessous et que vous chercherez à résoudre.

Mise en place☘

L'objectif de l'exercice est de mettre en place une modélisation d'un jeu de labyrinthe en langage Python.

On décide de représenter un labyrinthe par une matrice carrée de taille n*n, dans lequel les cases seront des 0 si l'on peut s'y déplacer et des 1 s'il s'agit d'un mur.

Exemple

Le code:

laby = [[0,1,1,1,1,1,1,1,1,1],
        [0,0,0,0,0,0,0,1,0,1],
        [1,0,1,1,1,1,0,1,0,1],
        [1,0,1,0,0,0,0,0,0,1],
        [1,0,1,1,1,1,1,0,1,1],
        [1,0,1,0,0,0,1,0,1,1],
        [1,0,1,0,1,0,1,0,1,1],
        [1,0,1,1,1,0,1,0,1,1],
        [1,0,0,0,0,0,1,0,0,1],
        [1,1,1,1,1,1,1,1,0,0]]

représente le labyrinthe:

L'entrée du labyrinthe se situe à la première case de la matrice (en haut à gauche).
La sortie du labyrinthe se trouve à la dernière case de la matrice (en bas à droite).

Question☘

Proposer une fonction mur en langage Python

prenant en paramètres une matrice (n lignes et n colonnes) représentant un labyrinthe et deux entiers i et j compris entre 0 et n-1,
renvoyant le booléen True en cas de présence d'un mur dans la cellule de coordonnées (ligne, colonne) = (i,j), et False en l'absence de mur dans cette cellule.

Exemples.

>>> mur(laby, 0, 1)
True
>>> mur(laby, 1, 0)
False

Solution

def mur(labyrinthe, i, j):
    return labyrinthe[i][j] == 1

Parcours☘

Un parcours dans le labyrinthe va être représenté par une liste de cases: il s'agit de couples (i, j) où i et j sont les numéros de ligne et colonne des cases visitées le long du parcours, deux cases successives dans la liste devant être adjacentes dans le labyrinthe.

Exemples.

La liste [(1,4), (1,5), (1,6), (2,6), (3,6), (3,5), (3,4)] correspond au parcours repéré par des étoiles ci-dessous:
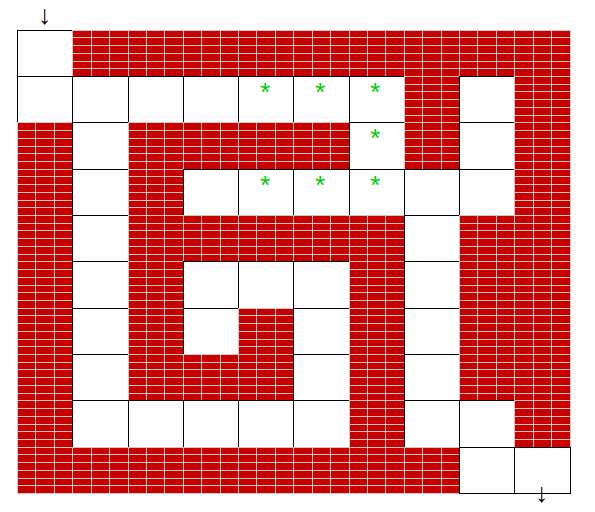
La liste [(0,0), (1,0), (1,1), (5,1), (6,1)] ne correspond pas à un parcours dans le labyrinthe car les deux cases (1,1) et (5,1) qui se suivent dans la liste ne sont pas adjacentes dans le labyrinthe.

On considère la fonction voisine ci-dessous (écrite en Python). Elle prend en paramètres deux cases données sous forme de couple.

def voisine(case1, case2):
    ligne1, colonne1 = case1
    ligne2, colonne2 = case2
    d = (ligne1-ligne2)**2 + (colonne1-colonne2)**2
    return d == 1

Question☘

Expliquer pourquoi la fonction voisine indique si les deux cases données en argument sont adjacentes.

Solution

Si ligne1 = ligne2, on a d = (colonne1-colonne2)**2.
- Cas 1: colonne1 = colonne2. On a alors d = 0 et les cases ne sont pas voisines (elles sont identiques).
- Cas 2: colonne1-colonne2 = 1 ou -1. Dans ce cas les cases sont voisines et d vaut 1.
- Cas 3: l'écart entre colonne1 et colonne2 est d'au moins 2. Dans ce cas, les cases ne sont pas voisines et d > 1.
Si ligne1-ligne2 est égal à 1 ou -1.
- Cas 1: colonne1 = colonne2. On est dans un cas de cases voisines et d vaut 1.
- Cas 2: colonne1 et colonne2 diffère d'au moins 1. On a dans ce d > 1 (car somme de deux termes tous deux au moins égaux à 1) et les cases ne sont pas voisines.
Si l'écart entre ligne1 et ligne2 est d'au moins 2, les cases ne sont pas voisines et d > 1.

Dans tous les cas, on constate que l'on a d = 1 pour des cases voisines et d $\neq$ 1 pour des cases non voisines. La fonction renvoie donc True dans le cas de cases voisines et False sinon.

Question☘

En déduire une fonction adjacentes qui prend en paramètre une liste de cases et renvoie le booléen True si la liste des cases forme une chaîne de cases adjacentes (et renvoie False sinon).

Exemples.

>>> adjacentes([(1,4), (1,5), (1,6), (2,6), (3,6), (3,5), (3,4)])
True
>>> adjacentes([(0,0), (1,0), (1,1), (5,1), (6,1)])
False

Solution

def adjacentes(liste_cases):
    for i in range(len(liste_cases)-1):
        if not voisine(liste_cases[i], liste_cases[i+1]):
            return False
    return True

Compatible☘

Une liste de cases sera qualifiée de parcours compatible avec le labyrinthe lorsqu'il s'agit d'une succession de cases adjacentes accessibles (non murées).

On donne la fonction teste(cases, labyrinthe) qui renvoie True si la liste de cases cases est un parcours compatible avec le labyrinthe labyrinthe (et renvoie False sinon).

def teste(cases, labyrinthe):
    if not adjacentes(cases):
        return False
    possible = True
    i = 0
    while i < len(cases) and possible:
        if mur(labyrinthe, cases[i][0], cases[i][1]):
            possible = False
        i = i+1
    return possible

Question☘

Justifier que la boucle de la fonction teste se termine.

Solution

La variable i ne peut prendre qu'un nombre fini de valeurs distinctes (les valeurs entre 0 et len(cases))
et cette variable ne prend jamais deux fois la même valeur (puisque i augmente strictement à chaque passage de la boucle avec l'instruction i = i+1).

La boucle se termine donc nécessairement.

Si l'on cherche à rédiger avec la notion de variant telle qu'on l'a utilisée dans le cours sur ce sujet, on utilise v = len(cases)-i.

v ne prend que des valeurs entières (différence de deux entiers)
v décroît strictement entre deux passages dans la boucle (car i augmente et len(cases) reste inchangé).

v est donc un variant de la boucle et la boucle termine.

Question☘

En déduire une fonction echappe(liste_cases, labyrinthe) qui renvoie True si la liste de cases liste_cases permet d'aller de l'entrée à la sortie du labyrinthe labyrinthe (et renvoie False sinon).

Exemples.

>>> liste = [(0,0), (1,0), (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,6), 
(3,6), (3,7), (4,7), (5,7), (6,7), (7,7), (8,7), (8,8), (9,8), (9,9)]
>>> echappe(liste, laby)
True
>>> liste2 =  [(0,0),  (9,9)]
>>> echappe(liste, laby)
False

Solution

def echappe(liste_cases, labyrinthe):
    n = len(labyrinthe)
    if not teste(liste_cases, labyrinthe):
        return False
    if liste_cases[0] != (0,0):
        return False
    if liste_cases[-1] != (n-1, n-1):
        return False
    return True