Pollutions☘
Sur une carte, on a délimité des zones à l'aide d'une grille, certaines régions (cellules de la grille) ont été polluées par des radiations dangereuses. L'objectif sera de déterminer les régions (cellules) les plus éloignées de ces régions devenues malsaines.
Affichage☘
Pour afficher la carte (grille), on utilisera ici une représentation obtenue à l'aide de la tortue python.
On vous propose ci-dessous un script python, votre mission est de comprendre ce code à l'aide de la documentation du module turtle puis de l'utiliser sur un ou deux exemples.
Le fichier tortue_affiche_matrice.py permet d'afficher une matrice.
texte du fichier d'affichage
En vous aidant de la documentation du module turtle, cherchez à comprendre le rôle de chaque instruction du code ci-dessous.
from turtle import *
def affiche_matrice(tab, unite=10):
delay(0)
nb_lignes = len(tab)
nb_colonnes = len(tab[0])
setworldcoordinates(-1*unite,-1*unite, (nb_colonnes+1)*unite, (nb_lignes+1)*unite)
hideturtle()
# tracé des horizontales:
penup()
goto(0,0)
pendown()
for ligne in range(nb_lignes+1):
forward(nb_colonnes * unite)
penup()
goto(0, (ligne+1)*unite)
pendown()
# tracé des verticales:
penup()
goto(0,0)
pendown()
setheading(90)
for colonne in range(nb_colonnes+1):
forward(nb_lignes * unite)
penup()
goto((colonne+1)*unite, 0)
pendown()
# numérotation des colonnes
penup()
goto(unite/2,-unite/3)
pendown()
for colonne in range(nb_colonnes):
write(colonne,align="center", font=("Arial", 8, "normal"))
penup()
goto((colonne+1)*unite+unite/2, -unite/3)
pendown()
# numérotation des lignes
penup()
goto(-unite/2,unite/2)
pendown()
for ligne in range(nb_lignes):
write(nb_lignes-1-ligne,align="right", font=("Arial", 8, "normal"))
penup()
goto(-unite/2, (ligne+1)*unite+unite/2)
pendown()
# remplissage des cellules
for ligne in range(nb_lignes):
for colonne in range(nb_colonnes):
penup()
goto(colonne*unite+unite/2, (nb_lignes-1-ligne)*unite+unite/3)
write(tab[ligne][colonne], align="center", font=("Arial", 20, "normal"))
mainloop()
Testez cet affichage avec un ou deux exemples.
Un appel possible
from tortue_affiche_matrice import affiche_matrice
matrice = [ [ i-j for j in range(5)] for i in range(7)]
affiche_matrice(matrice)
Une illustration avec les régions polluées
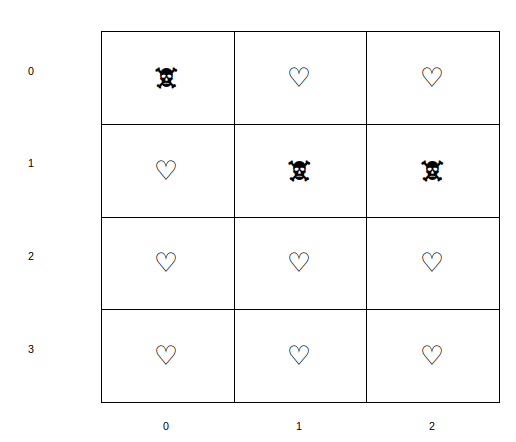
Une région portant le symbole 🕱 (vous pouvez utiliser ☠ si le premier caractère skull ne s'affiche pas) est une région polluée. Une zone portant le symbole ♡ est une zone préservée.
Une telle carte sera représentée en python par le code suivant:
carte = [['🕱','♡', '♡'],
['♡','🕱', '🕱'],
['♡','♡','♡'],
['♡','♡','♡']]
Distance entre deux régions☘
On ne peut se déplacer entre régions qu'en passant d'une région (une case) à une case voisine (c'est à dire une case ayant un côté commun avec la précédente, un sommet commun ne suffit pas).
La distance entre deux régions est le nombre de frontières à traverser pour aller de l'une à l'autre.
Par exemple, la distance entre les deux cases 🕱 ci-dessous (case ligne=0, colonne=0 et case ligne=4, colonne=2) est égale à 6.
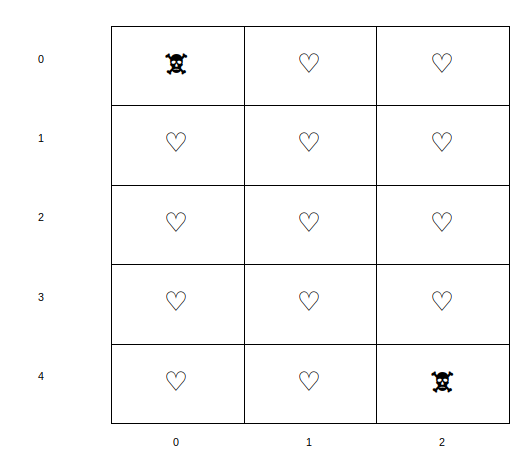
On obtient cette distance comme suit:
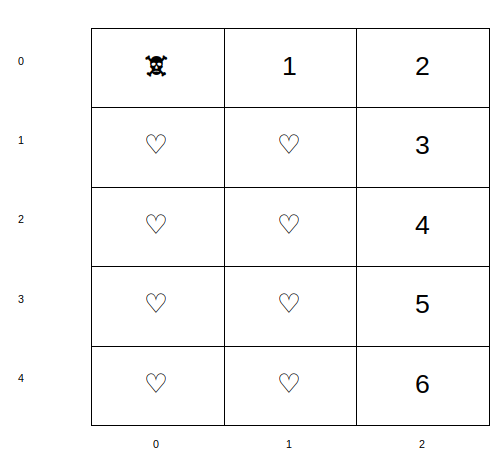
ou comme suit:
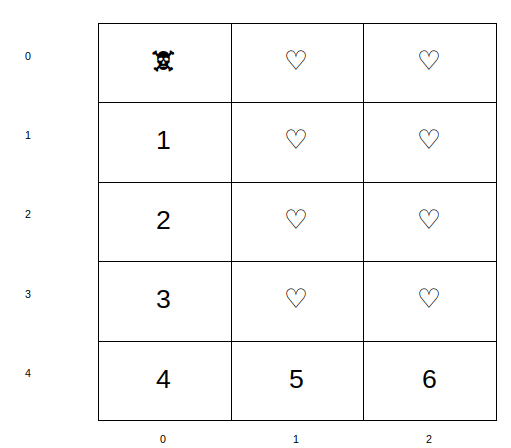
ou encore...
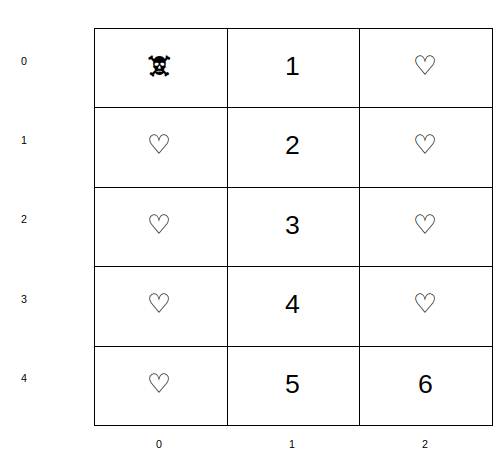
L'important est de passer d'une cellule à une autre ayant un côté commun (les déplacements sont donc horizontaux ou verticaux mais pas en diagonal).
Cette distance est également ce que l'on appelle la distance Manhattan.
Proposer un corps pour la fonction Python suivante:
def manhattan(a,b, p,q):
"""
(a,b) -- coordonnées (ligne, colonne) d'une cellule
(p,q) -- coordonnées (ligne, colonne) d'une cellule
renvoie la distance manhattan entre ces deux cellules
"""
Rappel
On rappelle que le langage python définit
la fonction valeur absolue abs.
Solution
def manhattan(a,b, p,q):
"""
(a,b) -- coordonnées (ligne, colonne) d'une cellule
(p,q) -- coordonnées (ligne, colonne) d'une cellule
renvoie la distance manhattan entre ces deux cellules
"""
return abs(a-p)+abs(b-q)
Distance aux pollutions☘
Pour définir la distance entre une région A et les pollutions:
- on calcule toutes les distances entre la région A et une région polluée de la carte.
- on prend la plus courte de ces distances.
La distance d'une case polluée aux pollutions est bien entendu égale à 0.
Écrire un corps possible pour la fonction suivante:
def distance_aux_pollutions(grille, a,b):
"""
grille -- matrice, chaque cellule contenant '🕱' ou '♡'
(a,b) -- couple (ligne, colonne) d'une cellule
renvoie la distance manhattan minimale
de la cellule (a,b) à une case '🕱' de grille.
"""
Solution
Un code possible:
def distance_aux_pollutions(grille, a,b):
"""
grille -- matrice, chaque cellule contenant '🕱' ou '♡'
(a,b) -- couple (ligne, colonne) d'une cellule
renvoie la distance manhattan minimale
de la cellule (a,b) à une case '🕱' de grille.
"""
largeur = len(grille[0]) # nombre de colonnes de la grille
hauteur = len(grille) # nombre de lignes de la grille
mini = manhattan(a,b, 0, 0)
for col in range(0,largeur):
for lig in range(0, hauteur):
if grille[lig][col] == '🕱':
dist = manhattan(a,b, lig, col)
if dist < mini:
mini = dist
return mini
Il est préférable de découper ce code en deux fonctions bien séparées:
- une fonction qui renvoie la valeur minimale d'une liste d'entiers.
- une fonction qui construit la liste des distances d'une région donnée aux régions polluées.
def minimum(liste):
"""
liste: liste d'entiers
renvoie la valeur minimale contenue dans liste
"""
mini = liste[0]
for valeur in liste:
if valeur < mini:
mini = valeur
return mini
def distance_aux_pollutions(grille, a,b):
"""
grille -- matrice, chaque cellule contenant '🕱' ou '♡'
(a,b) -- couple (ligne, colonne) d'une cellule
renvoie la distance manhattan minimale de la cellule (a,b) à une case '🕱' de grille
"""
liste_distances = []
for col in range(0,len(grille[0])):
for lig in range(0, len(grille)):
if grille[lig][col] == '🕱':
liste_distances.append(manhattan(a,b, lig, col))
return minimum(liste_distances)
Un test
>>> B = [['🕱','♡', '♡'],
['♡','🕱', '🕱'],
['♡','♡','♡'],
['♡','♡','♡']]
>>> distance_aux_pollutions(B,3,1)
2
On obtient une distance au mal égale à 2 pour la région ♥ (ligne=3, colonne=1):
elle est en effet à une distance 2 de la case 🕱 ligne=1, colonne=1 (repérée ci-dessous par ⚠)
et c'est la plus proche des cases 🕱.
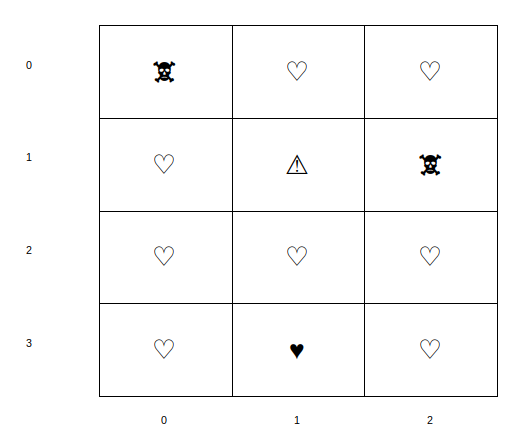
Recherche d'un abri☘
Pour se protéger, on décide de migrer vers une zone moins menacée.
Cette migration se fait vers une région dont la distance aux pollutions est la plus élevée.
Ecrire une fonction prenant en entrée une grille (contenant des '🕱' et des '♡') et renvoyant les coordonnées d'une cellule dont la distance aux pollutions est la plus grande possible.
Indication
Commencer par créer une fonction qui renverra une grille contenant, pour chaque cellule, sa distance aux pollutions.
Solution pour une grille intermédiaire
Fabrication de la grille intermédiaire présentée dans l'indication précédente:
def grille_dist_pollutions(grille):
largeur = len(grille[0]) # nombre de colonnes de la grille
hauteur = len(grille) # nombre de lignes de la grille
D = [[0 for k in range(largeur)] for j in range(hauteur)]
for lig in range(0, hauteur):
for col in range(0,largeur):
D[lig][col] = distance_aux_pollutions(grille, lig,col)
return D
Testons la fonction grille_dist_pollutions
On va tester la fonction sur la carte suivante:
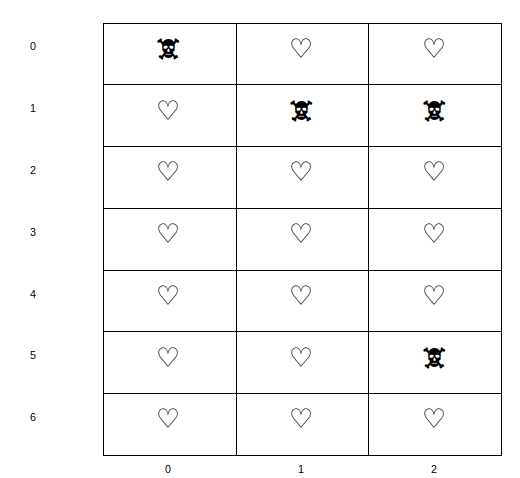
qui devrait donner (vérifiez "à la main"):
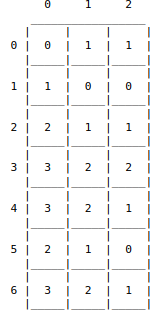
Dans cette situation, il y aura trois régions possibles comme choix de zone migratoire (les cellules à une distance 3 des régions polluées).
Solution
Pour choisir une région "sécurisée" (c'est à dire à distance maximale des pollutions), on recherche les cases (de la matrice des distances précédemment calculée) qui contiennent une valeur maximale. On renvoie l'une quelconque de ces cases (sous la forme d'un couple (ligne, colonne)).
Un code possible:
def cellule_refuge(grille):
"""
renvoie les coordonnées d'une cellule parmi les plus éloignées
de toute région polluée.
"""
# la matrice des distances aux pollutions:
largeur = len(grille[0]) # nombre de colonnes de la grille
hauteur = len(grille) # nombre de lignes de la grille
D = grille_dist_pollutions(grille)
# calcul des coordonnées d'une cellule
# d'éloignement aux pollutions maximal:
maxi = D[0][0]
cellule = (0,0)
for lig in range(0, hauteur):
for col in range(0,largeur):
dist = D[lig][col]
if dist > maxi:
maxi = dist
cellule = (lig, col)
return cellule
Un fichier ipynb (jupyter notebook) reprenant tout le code et la version statique html.