Des automates cellulaires☘

Dans cet exercice, on travaille sur les listes de listes.

L'un des objectifs sera d'obtenir des images comme celle-ci (au dernier paragraphe):

Fonction cree_matrice☘

Écrire un code python possible pour le corps de la fonction suivante:

def cree_matrice(n):
    """
    n:  entier >= 1

    renvoie une matrice carrée (2n+1)*(2n+1) avec un 1 au centre 
    et des 0 partout ailleurs.
    """

Solution

Un code possible:

def cree_matrice(n):
    """
    n:  entier >= 1

    renvoie une matrice carrée (2n+1)*(2n+1) avec un 1 au centre 
    et des 0 partout ailleurs.
    """
    mat = [[0 for col in range(2*n+1)] for lig in range(2*n+1)]
    mat[n][n] =  1
    return mat

Un code☘

Fonction dec_to_bin☘

Écrire un code python possible pour le corps de la fonction suivante:

def dec_to_bin(entier):
    """
    entier: entier naturel entre 0 et 1023

    renvoie une chaîne de 0 et 1
    correspondant à l'écriture binaire de entier.
    """

Solution

Il s'agit d'un code que vous devez connaître par coeur (divisions en cascade):

def dec_to_bin(entier):
    """
    entier: entier naturel entre 0 et 1023

    renvoie une chaîne de 0 et 1
    correspondant à l'écriture binaire de entier.
    """
    if entier == 0: return '0'
    chaine_bin = ''
    while entier != 0:
        chaine_bin = str(entier%2) + chaine_bin
        entier = entier//2
    return chaine_bin

Fonction bin_to_code☘

Écrire un code python possible pour le corps de la fonction suivante:

def bin_to_code(chaine_bin):
    """
    chaine_bin: chaîne de 0 et 1 de longueur <= 10

    renvoie la chaîne avec d'éventuels 0 à gauche pour que cette chaîne
    ait  une longueur égale à 10.

    >>> bin_to_code('1101')
    '0000001101'
    """

Solution

Un code possible:

def bin_to_code(chaine_bin):
    """
    chaine_bin: chaîne de 0 et 1 de longueur <= 10

    renvoie la chaîne avec d'éventuels 0 à gauche pour que cette chaîne
    ait  une longueur égale à 10.

    >>> bin_to_code('1101')
    '0000001101'
    """
    lg = len(chaine_bin)
    while lg != 10:
        chaine_bin = '0' + chaine_bin
        lg += 1
    return chaine_bin

Fonction dec_to_code☘

Écrire un code python possible pour le corps de la fonction suivante:

def dec_to_code(entier):
    """
    entier: entier naturel entre 0 et 1023

    renvoie une chaîne de 0 et 1 de longueur 10
    correspondant à l'écriture binaire de entier 
    (avec d'éventuels 0 à gauche pour obtenir la longueur 10)
    """

Solution

Un code possible:

def dec_to_code(entier):
    """
    entier: entier naturel entre 0 et 1023

    renvoie une chaîne de 0 et 1 de longueur 10
    correspondant à l'écriture binaire de entier 
    (avec d'éventuels 0 à gauche pour obtenir la longueur 10)
    """
    return bin_to_code(dec_to_bin(entier))

Des voisins☘

Écrire un code python possible pour le corps de la fonction suivante:

def nb_voisins1(matrice, xcellule, ycellule):
    """
    matrice: matrice carrée contenant uniquement des 0 et des 1
    xcellule, ycellule: coordonnées d'une cellule de la matrice

    renvoie le nombre de voisins de cellule qui  contiennent 1 
    (parmi les 4 voisins ayant un "côté" commun dans une représentation classique de la matrice
    sous forme d'un tableau)
    """

On ne traitera pas les cellules du bord (colonne 0, dernière colonne, ligne 0, dernière ligne).

Solution

Un code possible:

def nb_voisins1(matrice, xcellule, ycellule):
    """
    matrice: matrice carrée contenant uniquement des 0 et des 1
    xcellule, ycellule: coordonnées d'une cellule de la matrice

    renvoie le nombre de voisins de cellule qui  contiennent 1 
    (parmi les 4 voisins ayant un "côté" commun dans une représentation classique de la matrice
    sous forme d'un tableau)
    """
    compteur = 0
    if matrice[xcellule-1][ycellule] == 1: compteur += 1
    if matrice[xcellule][ycellule-1] == 1: compteur += 1
    if matrice[xcellule][ycellule+1] == 1: compteur += 1
    if matrice[xcellule+1][ycellule] == 1: compteur += 1
    return compteur

Lecture du code☘

On dispose d'une matrice carrée (en python, on utilisera une liste de listes), chaque cellule contenant 0 ou 1 (cf la fonction cree_matrice précédente).

On veut transformer chaque cellule en 0 ou 1 suivant ce que contient la cellule et le nombre de cellules égales à 1 parmi les voisines.

On va utiliser les écritures binaires de longueur 10 des questions précédentes comme des règles de transformation des 0 et des 1 de chaque cellule.

La fonction suivante traduit le principe du codage utilisé pour nos règles de transformations:

def transfo_cell(matrice, xcellule, ycellule, regle):
    """
    regle: entier entre 0 et 1023
    matrice: matrice carrée
    xcellule, ycellule: coordonnées d'une cellule de la matrice

    renvoie 0 ou 1 suivant la règle regle.
    """
    nb1 = nb_voisins1(matrice, xcellule, ycellule)
    regle = dec_to_code(regle)
    if matrice[xcellule][ycellule] == 0: 
        return int(regle[2 * nb1])
    else: 
        return int(regle[2 * nb1 + 1])

Remarque: on ne traite pas les cellules du bord (colonne 0, dernière colonne, ligne 0, dernière ligne).

Question 1☘

Si la cellule de coordonnées (xcellule, ycellule) a trois voisins marqués 1, comment sera-t-elle modifiée

si elle contient un 0 (par exemple la cellule centrale de cette configuration: )
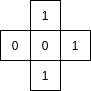si elle contient un 1 (par exemple la cellule centrale de cette configuration: )

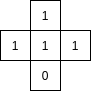avec la règle regle = 421.

Solution

Après l'instruction nb1 = nb_voisins1(matrice, xcellule, ycellule), nb1 désigne la valeur 3.

Après l'instruction regle = dec_to_code(regle), regle désigne la chaîne "0110100101".

Si la cellule contient un 0, la fonction renvoie int(regle[2 * nb1]), c'est à dire ici int(regle[6]) qui a pour valeur 0. La cellule reste donc 0.

Si la cellule contient un 1, la fonction renvoie int(regle[2 * nb1 + 1]), c'est à dire ici int(regle[7]) qui a pour valeur 1. La cellule reste donc 1.

Question 2☘

Si la cellule de coordonnées (xcellule, ycellule) a 1 voisin marqué 1, comment sera-t-elle modifiée

si elle contient un 0 (par exemple la cellule centrale de cette configuration: )
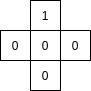si elle contient un 1 (par exemple la cellule centrale de cette configuration: )

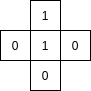avec la règle regle = 918.

Solution

Après l'instruction nb1 = nb_voisins1(matrice, xcellule, ycellule), nb1 désigne la valeur 1.

Après l'instruction regle = dec_to_code(regle), regle désigne la chaîne "1110010110".

Si la cellule contient un 0, la fonction renvoie int(regle[2 * nb1]), c'est à dire ici int(regle[2]) qui a pour valeur 1. La cellule devient 1.

Si la cellule contient un 1, la fonction renvoie int(regle[2 * nb1 + 1]), c'est à dire ici int(regle[3]) qui a pour valeur 0. La cellule devient donc 0.

Transformation de la matrice☘

Une étape☘

Écrire un code python possible pour le corps de la fonction suivante:

def etape(regle, matrice):
    """
    regle: entier entre 0 et 1023.
    matrice: matrice carrée ne contenant que des 0 et des 1.

    renvoie la matrice dans laquelle chaque cellule a été modifiée suivant la 
    règle regle.
    Attention: les valeurs des voisins à prendre en compte pour les transformations
    sur les valeurs  initiales de la matrice, tout doit se passer comme si toutes les 
    transformations étaient faites en même temps: en d'autres termes une cellule
    ne doit pas tenir compte de la nouvelle valeur d'une de ses voisines déjà transformée
    mais de la valeur de départ dans la donnée matrice.
    """

Remarque: on ne transformera pas les cellules du bord (colonne 0, dernière colonne, ligne 0, dernière ligne).

Solution

On a besoin de garder en mémoire les valeurs de départ de la matrice pour ne pas effectuer de transformation basée sur des cellules voisines déjà transformées.
Pour cela, attention, on a besoin de faire une copie profonde.

def etape(regle, matrice):
    """
    regle: entier entre 0 et 1023.
    matrice: matrice carrée ne contenant que des 0 et des 1.

    renvoie la matrice dans laquelle chaque cellule a été modifiée suivant la 
    règle regle.
    Attention: les valeurs des voisins à prendre en compte pour les transformations
    sur les valeurs  initiales de la matrice, tout doit se passer comme si toutes les 
    transformations étaient faites en même temps: en d'autres termes une cellule
    ne doit pas tenir compte de la nouvelle valeur d'une de ses voisines déjà transformée
    mais de la valeur de départ dans la donnée matrice.
    """
    nv_matrice = deepcopy(matrice)
    d = len(matrice)
    for lig in range(1, d-1):
        for col in range(1, d-1):
            nv_matrice[lig][col] = transfo_cell(matrice, col,  lig, regle)
    return nv_matrice

n étapes☘

Quel est alors le rôle de la fonction python suivante ?

def repet(n, regle):
    matrice = cree_matrice(n)
    for k in range(n):
        matrice = etape(regle, matrice)
    return matrice

Solution

Calculer la matrice après n étapes de transformation complète.

Utilisation pour créer une image☘

On interprète les 0 et les 1 de la matrice comme des indications de couleur de pixels d'une image carrée, par exemple avec le code suivant:

from PIL import Image

def cree_image(n, regle, couleur):

    # création de la matrice et transformations : 
    matrice = repet(n, regle)
    # dimension de la matrice carrée crée :
    d = 2*n+1

    # création d'une image de largeur d pixels et hauteur d pixels :
    imageBut = Image.new('RGB', (d, d)) 

    # on donne une couleur à chaque pixel : 
    for y in range(d) :
        for x in range(d) :
            if matrice[y][x] == 0:
                imageBut.putpixel((x,y), (255, 255, 255)) # (255,255,255) = blanc
            else:
                imageBut.putpixel((x,y), couleur) # couleur est un triplet (r,g,b)

    # sauvegarde de l'image créée :
    imageBut.save(f'repet{n}_regle{regle}.png')
    # on lance une visualisation :
    #imageBut.show()   # activer cette ligne pour ouvrir automatiquement l'image

Avec la règle 421, on obtient par exemple:

Avec 22 répétitions:
Avec 60 répétitions:
Avec 90 répétitions:

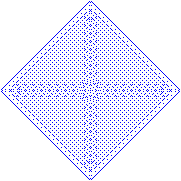
Faîtes d'autres tests !

Le code complet

from copy import deepcopy
from PIL import Image

def cree_matrice(n):
    """
    n:  entier >= 1

    renvoie une matrice carrée (2n+1)*(2n+1) avec un 1 au centre 
    et des 0 partout ailleurs.
    """
    mat = [[0 for col in range(2*n+1)] for lig in range(2*n+1)]
    mat[n][n] =  1
    return mat

def dec_to_bin(entier):
    """
    entier: entier naturel entre 0 et 1023

    renvoie une chaîne de 0 et 1
    correspondant à l'écriture binaire de entier.
    """
    if entier == 0: return '0'
    chaine_bin = ''
    while entier != 0:
        chaine_bin = str(entier%2) + chaine_bin
        entier = entier//2
    return chaine_bin

def bin_to_code(chaine_bin):
    """
    chaine_bin: chaîne de 0 et 1 de longueur <= 10

    renvoie la chaîne avec d'éventuels 0 à gauche pour que cette chaîne
    ait  une longueur égale à 10.

    >>> bin_to_code('1101')
    '0000001101'
    """
    lg = len(chaine_bin)
    while lg != 10:
        chaine_bin = '0' + chaine_bin
        lg += 1
    return chaine_bin

def dec_to_code(entier):
    """
    entier: entier naturel entre 0 et 1023

    renvoie une chaîne de 0 et 1 de longueur 10
    correspondant à l'écriture binaire de entier 
    (avec d'éventuels 0 à gauche pour obtenir la longueur 10)
    """
    return bin_to_code(dec_to_bin(entier))



def nb_voisins1(matrice, xcellule, ycellule):
    """
    matrice: matrice carrée contenant uniquement des 0 et des 1
    xcellule, ycellule: coordonnées d'une cellule de la matrice

    renvoie le nombre de voisins de cellule qui  contiennent 1 
    (parmi les 4 voisins ayant un "côté" commun dans une représentation classique de la matrice
    sous forme d'un tableau)
    """
    compteur = 0
    if matrice[xcellule-1][ycellule] == 1: compteur += 1
    if matrice[xcellule][ycellule-1] == 1: compteur += 1
    if matrice[xcellule][ycellule+1] == 1: compteur += 1
    if matrice[xcellule+1][ycellule] == 1: compteur += 1
    return compteur  

def transfo_cell(matrice, xcellule, ycellule, regle):
    """
    regle: entier entre 0 et 1023
    matrice: matrice carrée
    xcellule, ycellule: coordonnées d'une cellule de la matrice

    renvoie 0 ou 1 suivant la règle regle.
    """
    nb1 = nb_voisins1(matrice, xcellule, ycellule)
    regle = dec_to_code(regle)
    if matrice[xcellule][ycellule] == 0: 
        return int(regle[2 * nb1])
    else: 
        return int(regle[2 * nb1 + 1])


def etape(regle, matrice):
    """
    regle: entier entre 0 et 1023.
    matrice: matrice carrée ne contenant que des 0 et des 1.

    renvoie la matrice dans laquelle chaque cellule a été modifiée suivant la 
    règle regle.
    Attention: les valeurs des voisins à prendre en compte pour les transformations
    sur les valeurs  initiales de la matrice, tout doit se passer comme si toutes les 
    transformations étaient faites en même temps: en d'autres termes une cellule
    ne doit pas tenir compte de la nouvelle valeur d'une de ses voisines déjà transformée
    mais de la valeur de départ dans la donnée matrice.
    """
    nv_matrice = deepcopy(matrice)
    d = len(matrice)
    for lig in range(1, d-1):
        for col in range(1, d-1):
            nv_matrice[lig][col] = transfo_cell(matrice, col,  lig, regle)
    return nv_matrice


def repet(n, regle):
    matrice = cree_matrice(n)
    for k in range(n):
        matrice = etape(regle, matrice)
    return matrice

def cree_image(n, regle, couleur):
    matrice = repet(n, regle)
    d = 2*n+1
    imageBut = Image.new('RGB', (d, d))
    for y in range(d) :
        for x in range(d) :
            if matrice[y][x] == 0:
                imageBut.putpixel((x,y), (255, 255, 255))
            else:
                imageBut.putpixel((x,y), couleur)
    # sauvegarde de l'image créée :
    imageBut.save(f'repet{n}_regle{regle}.png')
    # on lance une visualisation :
    #imageBut.show()