Les dames☘
Attention
Page facultative, exercices d'entraînement.
Un problème classique☘
On dispose d'un échiquier. On veut placer 8 dames sur cet échiquier de façon à ce qu'aucune ne puisse en prendre une autre.
On rappelle que deux dames sont en prise si elles sont sur une même ligne, une même colonne ou une même diagonale.
Le problème est donc de placer 8 dames sur l'échiquier de façon à ce que deux dames quelconques ne soient jamais sur la même ligne, jamais sur la même colonne, jamais sur une même diagonale.
Vous pouvez lire la page wikipedia sur le sujet.
Voici une solution proposée sur cette page wikipedia:
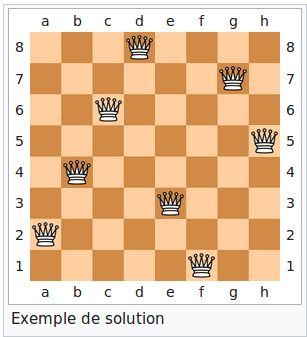
Exercice 1☘
On représente l'échiquier par une liste de listes.
dimension = 8
G = [[0 for j in range(dimension)] for i in range(dimension)]
G[i][j] = 0 signifiera que cette cellule ne contient pas de dame, G[i][j] = 1 signifiera que cette cellule contient une dame.
Vous devez écrire la fonction suivante:
def unDanslaligne(echiquier, ligne):
"""
echiquier -- matrice de 0 et de 1
ligne -- numéro de ligne dans cette matrice
renvoie True si la ligne contient un 1, False sinon.
"""
Vérifier que la ligne contient 1
Un code possible:
def unDanslaligne(echiquier, ligne):
"""
echiquier -- matrice de 0 et de 1
ligne -- numéro de ligne dans cette matrice
renvoie True si la ligne contient un 1, False sinon.
"""
for colonne in range(0, len(echiquier)-1):
if echiquier[ligne][colonne] == 1:
return True
return False
Tester la fonction! Pour cela créer des échiquiers avec quelques 1. Par exemple:
dimension = 8
G = [[0 for j in range(dimension)] for i in range(dimension)]
G[2][3] = 1
Exercice 2☘
On représente l'échiquier par une liste de listes.
dimension = 8
G = [[0 for j in range(dimension)] for i in range(dimension)]
G[i][j] = 0 signifiera que cette cellule ne contient pas de dame, G[i][j] = 1 signifiera que cette cellule contient une dame.
Vous devez écrire la fonction suivante:
def placeAuHasard(dimension):
"""
dimension -- entier naturel non nul
Renvoie un échiquier de taille dimension*dimension
dans lequel il y a un 1 unique dans chaque ligne et un 1 unique
dans chaque colonne.
"""
L'échiquier renvoyé contiendra un seul 1 par colonne mais aussi un seul 1 par ligne. Les emplacements des 1 seront choisis suivant le descriptif bref ci-dessous:
Pour chaque numéro de colonne:
choix d'une ligne au hasard.
Tant que cette ligne comporte déjà un 1, on choisit une autre ligne.
On place alors un 1 à l'intersection ligne, colonne.
Un code possible
from random import randint
def affichage(tab):
"""
tab -- liste de listes de nombres
affiche chaque liste en passant à la ligne entre les listes.
"""
for ligne in tab:
print(ligne)
def unDanslaligne(echiquier, ligne):
"""
echiquier -- matrice de 0 et de 1
ligne -- numéro de ligne dans cette matrice
renvoie True si la ligne contient un 1, False sinon.
"""
for colonne in range(0, len(echiquier)-1):
if echiquier[ligne][colonne] == 1:
return True
return False
def placeAuHasard(dimension):
"""
dimension -- entier naturel non nul
Renvoie un échiquier de taille dimension*dimension
dans lequel il y a un 1 unique dans chaque ligne et un 1 unique
dans chaque colonne.
"""
echiquier = [[0 for j in range(dimension)] for j in range(dimension)]
for colonne in range(dimension):
ligne = randint(0, dimension-1)
while unDanslaligne(echiquier, ligne):
ligne = randint(0, dimension-1)
echiquier[ligne][colonne] = 1
return echiquier
n = 8
affichage(placeAuHasard(n))
Exercice 3☘
Les couples de coordonnées d'un échiquier n×n (matrice n×n) sont les couples (tuple) (i, j) avec 0 ≤ i ≤ n-1 et 0 ≤ j ≤ n-1.
Écrire une fonction qui crée la liste de tous ces couples.
Un code possible
def listeCellules(dimension):
"""
dimension -- entier naturel non nul
Renvoie la liste des couples (i,j) avec 0 <= i <= dimension-1
et 0 <= j <= dimension-1.
Cette liste contient donc dimension**2 éléments.
"""
liste = []
for i in range(dimension):
for j in range(dimension):
liste.append((i,j))
return liste
par compréhension
La même fonction en utilisant une définition par compréhension:
def listeCellules(dimension):
"""
dimension -- entier naturel non nul
Renvoie la liste des couples (i,j) avec 0 <= i <= dimension-1
et 0 <= j <= dimension-1.
Cette liste contient donc dimension**2 éléments.
"""
return [(i,j) for i in range(dimension) for j in range(dimension)]
Exercice 4☘
Écrire un code pour la fonction spécifiée ainsi:
def cellulesSurMemeDiagonale(echiquier, cellule1, cellule2):
"""
echiquier -- matrice de 0 et de 1
cellule1 -- couple (ligne1, colonne1) ligne et colonne d'une cellule d'échiquier
cellule2 -- couple (ligne2, colonne2) ligne et colonne d'une cellule d'échiquier
Renvoie True si les deux cellules sont sur une même diagonale
et contiennent toutes deux la valeur 1,
False si elles ne sont pas sur la même diagonale
ou ne contiennent pas toutes deux 1.
"""
Note
Attention, ne vous limitez pas aux deux diagonales principales. Il faut vérifier toutes les diagonales.
Equation d'une diagonale
En considérant que les numéros des lignes et des colonnes sont en fait des ordonnées et des abscisses dans un repère, qu'en déduire pour caractériser les cellules d'une diagonale?
Les cellules d'une diagonale sont alignées donc ordonnée et abscisse sont liées par une relation affine... Il s'agit de déterminer des équations de droite. A vous de les trouver pour chacune des diagonales.
un code possible
Les diagonales ont des équations de la forme ligne + colonne = constante ou ligne - colonne = constante.
D'où un code possible:
from random import randint
def affichage(tab):
"""
tab -- liste de listes de nombres
affiche chaque liste en passant à la ligne entre les listes.
"""
for ligne in tab:
print(ligne)
def unDanslaligne(echiquier, ligne):
"""
echiquier -- matrice de 0 et de 1
ligne -- numéro de ligne dans cette matrice
renvoie True si la ligne contient un 1, False sinon.
"""
for colonne in range(0, len(echiquier)-1):
if echiquier[ligne][colonne] == 1:
return True
return False
def placeAuHasard(dimension):
"""
dimension -- entier naturel non nul
Renvoie un échiquier de taille dimension*dimension
dans lequel il y a un 1 unique dasn chaque ligne et un 1 unique
dans chaque colonne.
"""
echiquier = [[0 for j in range(dimension)] for j in range(dimension)]
for colonne in range(dimension):
ligne = randint(0, dimension-1)
while unDanslaligne(echiquier, ligne):
ligne = randint(0, dimension-1)
echiquier[ligne][colonne] = 1
return echiquier
def cellulesSurMemeDiagonale(echiquier, cellule1, cellule2):
"""
echiquier -- matrice de 0 et de 1
cellule1 -- couple (ligne1, colonne1) ligne et colonne d'une cellule d'échiquier
cellule2 -- couple (ligne2, colonne2) ligne et colonne d'une cellule d'échiquier
Renvoie True si les deux cellules sont sur une même diagonale et contiennent la valeur 1,
False sinon
"""
ligne1, colonne1 = cellule1[0], cellule1[1]
ligne2, colonne2 = cellule2[0], cellule2[1]
if ligne1 + colonne1 == ligne2 + colonne2:
if echiquier[ligne1][colonne1] == 1 and echiquier[ligne2][colonne2] == 1:
return True
if ligne1 - colonne1 == ligne2 - colonne2:
if echiquier[ligne1][colonne1] == 1 and echiquier[ligne2][colonne2] == 1:
return True
return False
# essais:
n = 4
A = placeAuHasard(n)
affichage(A)
print(cellulesSurMemeDiagonale(A, (0,0), (1,1)))
print(cellulesSurMemeDiagonale(A, (1,0), (2,1)))
Exercice 5☘
On dispose d'échiquiers comportant un 1 unique par ligne et par colonne.
Il faut maintenant vérifier qu'il n'y a qu'un seul 1 par diagonale.
Écrire une fonction prenant en paramètre un échiquier de 0 et de 1 et vérifiant qu'il n'y a pas deux 1 sur une même diagonale.
Un code possible
from random import randint
def affichage(tab):
"""
tab -- liste de listes de nombres
affiche chaque liste en passant à la ligne entre les listes.
"""
for ligne in tab:
print(ligne)
def unDanslaligne(echiquier, ligne):
"""
echiquier -- matrice de 0 et de 1
ligne -- numéro de ligne dans cette matrice
renvoie True si la ligne contient un 1, False sinon.
"""
for colonne in range(0, len(echiquier)-1):
if echiquier[ligne][colonne] == 1:
return True
return False
def placeAuHasard(dimension):
"""
dimension -- entier naturel non nul
Renvoie un échiquier de taille dimension*dimension
dans lequel il y a un 1 unique dasn chaque ligne et un 1 unique
dans chaque colonne.
"""
echiquier = [[0 for j in range(dimension)] for j in range(dimension)]
for colonne in range(dimension):
ligne = randint(0, dimension-1)
while unDanslaligne(echiquier, ligne):
ligne = randint(0, dimension-1)
echiquier[ligne][colonne] = 1
return echiquier
def listeCellules(dimension):
"""
dimension -- entier naturel non nul
Renvoie la liste des couples (i,j) avec 0 <= i <= dimension-1
et 0 <= j <= dimension-1.
Cette liste contient donc dimension**2 éléments.
"""
return [(i,j) for i in range(dimension) for j in range(dimension)]
def cellulesSurMemeDiagonale(echiquier, cellule1, cellule2):
"""
echiquier -- matrice de 0 et de 1
cellule1 -- couple (ligne1, colonne1) ligne et colonne d'une cellule d'échiquier
cellule2 -- couple (ligne2, colonne2) ligne et colonne d'une cellule d'échiquier
Renvoie True si les deux cellules sont sur une même diagonale et contiennent la valeur 1,
False sinon
"""
ligne1, colonne1 = cellule1[0], cellule1[1]
ligne2, colonne2 = cellule2[0], cellule2[1]
if ligne1 + colonne1 == ligne2 + colonne2:
if echiquier[ligne1][colonne1] == 1 and echiquier[ligne2][colonne2] == 1:
return True
if ligne1 - colonne1 == ligne2 - colonne2:
if echiquier[ligne1][colonne1] == 1 and echiquier[ligne2][colonne2] == 1:
return True
return False
def diagonaleSansDouble1(echiquier):
"""
echiquier -- matrice de 0 et de 1
renvoie True si aucune diagonale n'a plus d'un 1, False sinon
"""
dimension = len(echiquier)
cellules = listeCellules(dimension)
for cellule1 in cellules:
for cellule2 in cellules:
if cellule2 != cellule1:
if cellulesSurMemeDiagonale(echiquier, cellule1, cellule2):
return False
return True
n = 8
A = placeAuHasard(n)
affichage(A)
print(diagonaleSansDouble1(A))
Exercice 6☘
Écrire maintenant une fonction qui génère au hasard un échiquier par la fonction placeAuHasard de l'exercice précédent en recalculant un échiquier au hasard tant que celui-ci comporte des diagonales avec plusieurs 1.
Un code
Un code possible:
from random import randint
def affichage(tab):
"""
tab -- liste de listes de nombres
affiche chaque liste en passant à la ligne entre les listes.
"""
for ligne in tab:
print(ligne)
def unDanslaligne(echiquier, ligne):
"""
echiquier -- matrice de 0 et de 1
ligne -- numéro de ligne dans cette matrice
renvoie True si la ligne contient un 1, False sinon.
"""
for colonne in range(0, len(echiquier)-1):
if echiquier[ligne][colonne] == 1:
return True
return False
def placeAuHasard(dimension):
"""
dimension -- entier naturel non nul
Renvoie un échiquier de taille dimension*dimension
dans lequel il y a un 1 unique dasn chaque ligne et un 1 unique
dans chaque colonne.
"""
echiquier = [[0 for j in range(dimension)] for j in range(dimension)]
for colonne in range(dimension):
ligne = randint(0, dimension-1)
while unDanslaligne(echiquier, ligne):
ligne = randint(0, dimension-1)
echiquier[ligne][colonne] = 1
return echiquier
def listeCellules(dimension):
"""
dimension -- entier naturel non nul
Renvoie la liste des couples (i,j) avec 0 <= i <= dimension-1
et 0 <= j <= dimension-1.
Cette liste contient donc dimension**2 éléments.
"""
liste = []
for i in range(dimension):
for j in range(dimension):
liste.append((i,j))
return liste
def listeCellules(dimension):
"""
dimension -- entier naturel non nul
Renvoie la liste des couples (i,j) avec 0 <= i <= dimension-1
et 0 <= j <= dimension-1.
Cette liste contient donc dimension**2 éléments.
"""
return [(i,j) for i in range(dimension) for j in range(dimension)]
def cellulesSurMemeDiagonale(echiquier, cellule1, cellule2):
"""
echiquier -- matrice de 0 et de 1
cellule1 -- couple (ligne1, colonne1) ligne et colonne d'une cellule d'échiquier
cellule2 -- couple (ligne2, colonne2) ligne et colonne d'une cellule d'échiquier
Renvoie True si les deux cellules sont sur une même diagonale et contiennent la valeur 1,
False sinon
"""
ligne1, colonne1 = cellule1[0], cellule1[1]
ligne2, colonne2 = cellule2[0], cellule2[1]
if ligne1 + colonne1 == ligne2 + colonne2:
if echiquier[ligne1][colonne1] == 1 and echiquier[ligne2][colonne2] == 1:
return True
if ligne1 - colonne1 == ligne2 - colonne2:
if echiquier[ligne1][colonne1] == 1 and echiquier[ligne2][colonne2] == 1:
return True
return False
def diagonaleSansDouble1(echiquier):
"""
echiquier -- matrice de 0 et de 1
renvoie True si aucune diagonale n'a plus d'un 1, False sinon
"""
dimension = len(echiquier)
cellules = listeCellules(dimension)
for cellule1 in cellules:
for cellule2 in cellules:
if cellule2 != cellule1:
if cellulesSurMemeDiagonale(echiquier, cellule1, cellule2):
return False
return True
def genereSolution(dimension):
echiquier = placeAuHasard(dimension)
while not diagonaleSansDouble1(echiquier):
echiquier = placeAuHasard(dimension)
return echiquier
# ESSAI
n = 8
affichage(genereSolution(n))
Exemple de solution trouvée avec ce programme:
[0, 0, 1, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 1]
[1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1, 0]
[0, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0, 0, 0]
Remarque
On a ainsi généré au hasard une solution du problème des 8 dames non en prises sur un échiquier... Ce qui serait intéressant serait de générer la liste de toutes les solutions. Pour cela, les notions du programme de terminale (parcours d'arbre, récursivité) seront tout à fait adaptées.